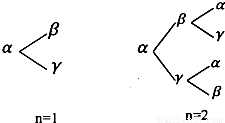
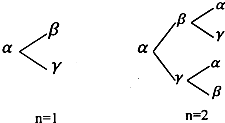用α、β、γ三个字母组成一个长度为（n+1）（n∈N^*）个字母的字符串，要求由α开始，相邻两个字母不同．例如：n=1时，排出的字符串是αβ或αγ；n=2时，排出的字符串是αβα、αβγ、αγα、αγβ（如图）．若记这种（n+1）个字符串中，最后一个字母仍是α的字符串的个数为a_n，可知a₁=0，a₂=2，a₃=2，a₄=6，…，则数列{a_n}的第n项a_n与第n-1项a_n-1（n≥2，n∈N^*）    ．

已知点P是直角坐标平面内的动点，点P到直线l₁：x=-2的距离为d₁，到点F（-1，0）的距离为d₂，且

d2

d1

=

2

2

．
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l₁：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
（3）记S₁=S_△FAM，S₂=S_△FMN，S₃=S_△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使S₂²=λS₁S₃成立．若存在，求出λ的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线l1：x=-

a2

c

、点F（-c，0）、曲线C：

x2

a2

+

y2

b2

=1(a＞b＞0，c=

a2-b2

)，则使等式S₂²=λS₁S₃成立的λ的值仍保持不变．请给出你的判断 （填写“不正确”或“正确”）（限于时间，这里不需要举反例，或证明）．

对命题“a∥b∥c推出a∥c”，关于真假问题，甲、乙两个学生的判断如下:甲生判断是真命题.理由是：由a∥b可知a与b的方向相同或相反,由b∥c可知c与b的方向相同或相反,从而有a与c的方向相同或相反,故a∥c,即原命题为真命题；乙生判断是假命题.理由是：当两个非零向量a,c不平行,而b=0时,显然a∥b且b∥c,但不能推出a∥b∥c,故此时结论不成立,即原命题为假命题.究竟甲、乙两生谁的判断正确呢？请给以分析.

已知两定点A(0，-1)，C(0，2)，动点M满足∠MCA=2∠MAC.

(Ⅰ)求动点M的轨迹Q的方程；

(Ⅱ)设曲线Q与y轴的交点为B，点B、F是曲线Q上两个不同的动点，且=0，直线AE与BF交于点P(x₀，y₀)，求证：为定值;

(Ⅲ)在第(Ⅱ)问的条件下，求证：过点p′(0，y₀)和点E的直线是曲线Q的一条切线.

(Ⅳ)在第(Ⅱ)问的条件下，试问是否存在点E使得(或)，若存在，求出此时点E的坐标；若不存在，说明理由.