
题目列表(包括答案和解析)
| 甲 | 乙 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
甲:19 20 21 23 25 29 32 33 37 41
乙:10 26 30 30 34 37 44 46 46 47
| 甲 | 乙 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
(1)用茎叶图表示上述两组数据,并对两块地抽取树苗的高度的平均数和中位数进行比较,写出两个统计结论;
(2)现苗圃基地将甲、乙两块地的树苗合在一起,按高度分成一、二两个等级,每个等级按不同的价格出售.某市绿化部门下属的2个单位计划购买甲、乙两地种植的树苗.已知每个单位购买每个等级树苗所需费用均为5万元,且每个单位对每个等级树苗买和不买的可能性各占一半,求该市绿化部门此次采购所需资金总额X的分布列及数学期望值E(X).
| 甲 | 乙 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
|
|
视觉记忆能力 |
||||
|
偏低 |
中等 |
偏高 |
超常 |
||
|
听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
|
中等 |
1 |
8 |
3 |
|
|
|
偏高 |
2 |
|
0 |
1 |
|
|
超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为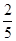 .
.
(I)试确定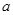 、
、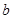 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为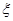 ,求随机变量
,求随机变量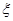 的数学期望
的数学期望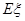 .
.
【解析】1)中由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有(10+a)人.记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,则P(A)=(10+a)/40=2/5,解得a=6.……………2分
所以.b=40-(32+a)=40-38=2答:a的值为6,b的值为2.………………3分
(2)中由表格数据可知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人.
方法1:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件B,
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件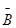
(3)中由于从40位学生中任意抽取3位的结果数为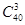 ,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为
,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为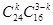 ,………………………7分
,………………………7分
所以从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的概率为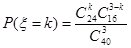 ,k=0,1,2,3
,k=0,1,2,3
 某厂制造A种电子装置45台,B种电子装置55台,为了给每台装置装配一个外壳,要从两种不同规格的薄钢板上截取.已知甲种薄钢板每张面积为2m2,可做A种外壳3个和B种外壳5个;乙种薄钢板每张面积为3m2,可做A种和B种外壳各6个,用这两种薄钢板各多少张,才能使总的用料面积最小?(请根据题意,在下面的横线处按要求填上恰当的关系式或数值)
某厂制造A种电子装置45台,B种电子装置55台,为了给每台装置装配一个外壳,要从两种不同规格的薄钢板上截取.已知甲种薄钢板每张面积为2m2,可做A种外壳3个和B种外壳5个;乙种薄钢板每张面积为3m2,可做A种和B种外壳各6个,用这两种薄钢板各多少张,才能使总的用料面积最小?(请根据题意,在下面的横线处按要求填上恰当的关系式或数值)
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com