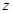关于的方程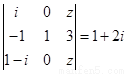(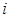是虚数单位)的解是＝　　　    　　　．

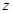设函数f(x)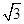＝cos²ωx＋sinωxcosωx＋a(其中ω>0，a∈R)，且f(x)的图象在y轴右侧的第一个最高点的横坐标为.

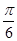(1)求ω的值；

(2)如果f(x)在区间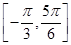上的最小值为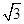，求a的值．

已知a＝(cos2α，sinα)，b＝(1,2sinα－1)，α∈(，π)，若a·b＝，则tan(α＋)的值是(       )

A.               B.             C.               D.

在△ABC中，若sinBsinC＝cos²，则△ABC是(　　)

A．等边三角形                 B．等腰三角形

C．不等边三角形              D．直角三角形

给出下列四个结论：

①“k＝1”“是函数y＝cos² k x－sin² k x的最小正周期为π”的充要条件.

②函数y＝sin（2 x－）沿向量a＝（，0）平移后所得图象的函数表达式是：

y＝cos2 x.

③函数y＝lg(a x²－2 a x＋1)的定义域是R，则实数a的取值范围是（0，1）.

④单位向量a、b的夹角是60°，则向量2a－b的模是.

其中不正确结论的序号是.(  )（填写你认为不正确的所有结论序号）