练习册

  • 练习册
  • 试题
    A． B． C． D．答案:B 【查看更多】

     

    题目列表(包括答案和解析)

    定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3，}，函数y=-x的“特征数”是{0，-1，0}
    （1）将“特征数”是{0，
    		3
    3
    ，1    }的函数图象向下平移2个单位，得到的新函数的解析式是
    y=
    		3
    3
    x-1
    y=
    		3
    3
    x-1
    ； （答案写在答卷上）
    （2）在（1）中，平移前后的两个函数分别与y轴交于A、B两点，与直线x=
    		3
    分别交于D、C两点，在平面直角坐标系中画出图形，判断以点A、B、C、D为顶点的四边形形状，并说明理由；
    （3）若（2）中的四边形与“特征数”是{1，-2b，b2+
    1
    2
    }的函数图象的有交点，求满足条件的实数b的取值范围．

    查看答案和解析>>

    定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3，}，函数y=-x的“特征数”是{0，-1，0}
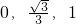    （1）将“特征数”是{数学公式}的函数图象向下平移2个单位，得到的新函数的解析式是________； （答案写在答卷上）
    （2）在（1）中，平移前后的两个函数分别与y轴交于A、B两点，与直线x=数学公式分别交于D、C两点，在平面直角坐标系中画出图形，判断以点A、B、C、D为顶点的四边形形状，并说明理由；
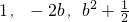    （3）若（2）中的四边形与“特征数”是{数学公式}的函数图象的有交点，求满足条件的实数b的取值范围．

    查看答案和解析>>

    铁矿石A和B的含铁率a ，冶炼每万吨铁矿石的的排放量b及每万吨铁矿石的价格c如下表：

    a

    b(万吨)

    c（百万元）

    A

    50％

    1

    3

    B

    70％

    0.5

    6

    某冶炼厂至少要生产1.9（万吨）铁，若要求的排放量不超过2（万吨）则购买铁矿石的最少费用为

    A．14　万元　　     B．15万元　     　C．20万元　　　   　D．以上答案都不对

    查看答案和解析>>

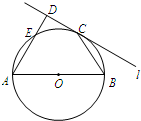    [选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
    A．（选修4-1：几何证明选讲）
    如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
    B．（选修4-2：矩阵与变换）
    已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
    1
    1
    ，特征值λ2=-1及其对应的一个特征向量α2=
    1
    -1
    ，求矩阵A的逆矩阵A-1．
    C．（选修4-4：坐标系与参数方程）
    以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，
    π
    2
    )    ，直线l过点A且倾斜角为
    π
    4
    ，圆C以点B为圆心，4为半径，试求直线l的参数方程和圆C的极坐标方程．
    D．（选修4-5：不等式选讲）
    设a，b，c，d都是正数，且x=
    		a2+b2
    ，y=
    		c2+d2
    ．求证：xy≥
    		(ac+bd)(ad+bc)
    ．

    查看答案和解析>>

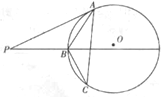    [选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
    A．（选修4-1：几何证明选讲）
    过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB=7，∠ABP=∠ABC，C是圆上一点使得BC=5，求线段AB的长．
    B．（选修4-2：矩阵与变换）
    求曲线C：xy=1在矩阵
    		2
    2
    		-
    		2
    2
    		2
    2
    		2
    2
    对应的变换作用下得到的曲线C′的方程．
    C．（选修4-4：坐标系与参数方程）
    已知曲线C1：
    x=3cosθ
    y=2sinθ
    （θ为参数）和曲线C2：ρsin（θ-
    π
    4
    ）=
    		2
    ．
    （1）将两曲线方程分别化成普通方程；
    （2）求两曲线的交点坐标．
    D．（选修4-5：不等式选讲）
    已知|x-a|＜
    c
    4
    ，|y-b|＜
    c
    6
    ，求证：|2x-3y-2a+3b|＜c．

    查看答案和解析>>


    同步练习册答案