
题目列表(包括答案和解析)
设函数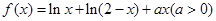 .
.
(Ⅰ) 当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
【解析】第一问中利用函数 的定义域为(0,2),
的定义域为(0,2), .
.
当a=1时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
第二问中,利用当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
解:函数 的定义域为(0,2),
的定义域为(0,2), .
.
(1)当 时,
时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
(2)当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
若 ,计算得当
,计算得当 时
时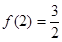 ,当
,当 时有
时有 ,
, ,
, ,
, ,因此猜测当
,因此猜测当 时,一般有不等式________________
时,一般有不等式________________
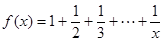 ,计算得当
,计算得当 时
时 ,当
,当 时有
时有 ,
, ,
, ,
, ,因此猜测当
,因此猜测当 时,一般有不等式________________
时,一般有不等式________________(1)由“若ab=ac(a≠0,a,b,c∈R),则b=c”;类比“若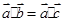 (
(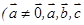 为三个向量),则
为三个向量),则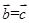 ”;
”;
(2)如果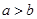 ,那么
,那么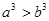 ;
;
(3)若回归直线方程为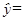 1.5x+45,x∈{1,5,7,13,19},则
1.5x+45,x∈{1,5,7,13,19},则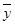 =58.5;
=58.5;
(4)当n为正整数时,函数N(n)表示n的最大奇因数,如N(3)=3,N(10)=5, ,由此可得函数N(n)具有性质:当n为正整数时,N(2n)= N(n),N(2n-1)=2n-1.
上述四个推理中,得出结论正确的是 (写出所有正确结论的序号).
(1)由“若ab=ac(a≠0,a,b,c∈R),则b=c”;类比“若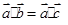 (
(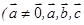 为三个向量),则
为三个向量),则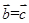 ”;
”;
(2)如果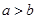 ,那么
,那么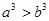 ;
;
(3)若回归直线方程为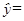 1.5x+45,x∈{1,5,7,13,19},则
1.5x+45,x∈{1,5,7,13,19},则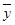 =58.5;
=58.5;
(4)当n为正整数时,函数N(n)表示n的最大奇因数,如N(3)=3,N(10)=5, ,由此可得函数N(n)具有性质:当n为正整数时,N(2n)= N(n),N(2n-1)=2n-1.
上述四个推理中,得出结论正确的是 (写出所有正确结论的序号).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com