
题目列表(包括答案和解析)
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
 |
| y |
| |||||||
|
. |
| y |
. |
| x |
. |
| x |
. |
| y |
| 8 |
 |
| i=1 |
. |
| x |
| 8 |
 |
| i=1 |
. |
| x |
. |
| y |
| 1050 |
| 457 |
| 550 |
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(2)随机抽取8位同学,数学分![]() 数依次为:60,65,70,75,80,85,90,95;
数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定90分(含90分)以上为优秀,记![]() 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若这8位同学的数学、物理分数事实上对应下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7[来源:Z#xx#k.Com] | 8 |
| 数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数 | 72 | 77 | 80[来源:学科网] | 84 | 88 | 90 | 93 | 95 |
根据上表数据可知,变量![]() 与
与![]() 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出![]() 与
与![]() 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式:![]() ,其中
,其中 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(2)随机抽取8位同学,数学分数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定90分(含90分)以上为优秀,记 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求 的分布列和数学期望;
的分布列和数学期望;
②若这8位同学的数学、物理分数事实上对应下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7[来源:Z#xx#k.Com] |
8 |
|
数学分数 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
物理分数 |
72 |
77 |
80[来源:] |
84 |
88 |
90 |
93 |
95 |
根据上表数据可知,变量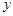 与
与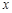 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出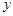 与
与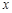 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式: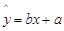 ,其中
,其中 ,
,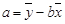 ;参考数据:
;参考数据: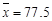 ,
,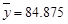 ,
, ,
,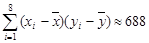 ,
, ,
,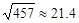 ,
,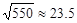 )
)
为考虑广告费用x与销售额y之间的关系,抽取了5家餐厅,得到如下数据:
|
广告费用(千元) |
1.0 |
4.0 |
6.0 |
10.0 |
14.0 |
|
销售额(千元) |
19.0 |
44.0 |
40.0 |
52.0 |
53.0 |
(1)在同一张图上画散点图,直线 (1)=24+2.5x,
(1)=24+2.5x, (2)=
(2)= ;
;
(2)比较所画直线与曲线,哪一条更能表现这组数据之间的关系?
(3)分别计算用直线方程与曲线方程得到在5个x点处的销售额预测值、预测值与实际预测之间的误差,最后比较两个误差绝对值之和的大小。
为考虑广告费用x与销售额y之间的关系,抽取了5家餐厅,得到如下数据:
| 广告费用(千元) | 1.0 | 4.0 | 6.0 | 10.0 | 14.0 |
| 销售额(千元) | 19.0 | 44.0 | 40.0 | 52.0 | 53.0 |
(1)在同一张图上画散点图,直线![]() (1)=24+2.5x,
(1)=24+2.5x,![]() (2)=
(2)=![]() ;
;
(2)比较所画直线与曲线,哪一条更能表现这组数据之间的关系?
(3)分别计算用直线方程与曲线方程得到在5个x点处的销售额预测值、预测值与实际预测之间的误差,最后比较两个误差绝对值之和的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com