
题目列表(包括答案和解析)
(14分)
已知数列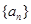 的前
的前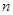 项和为
项和为 ,且对任意正整数
,且对任意正整数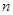 ,有
,有 ,
, ,
,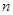 (
( ,
, )成等差数列,令
)成等差数列,令 。
。
(1)求数列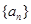 的通项公式
的通项公式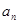 (用
(用 ,
,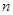 表示)
表示)
(2)当 时,数列
时,数列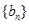 是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
(3)若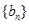 是一个单调递增数列,请求出
是一个单调递增数列,请求出 的取值范围。
的取值范围。
(14分) 已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,有
,有![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() )成等差数列,令
)成等差数列,令![]() 。
。
(1)求数列![]() 的通项公式
的通项公式![]() (用
(用![]() ,
,![]() 表示)
表示)
(2)当![]() 时,数列
时,数列![]() 是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
(3)若![]() 是一个单调递增数列,请求出
是一个单调递增数列,请求出![]() 的取值范围。
的取值范围。
(本小题满分l2分)
运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假
设汽油的价格是每升2元,而汽车每小时耗油(2+)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
(本小题共14分)已知函数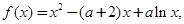 其中常数
其中常数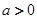 .
.
(1)当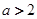 时,求函数
时,求函数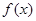 的单调递增区间;
的单调递增区间;
(2)当 时,若函数
时,若函数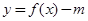 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围;
(3)设定义在D上的函数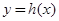 在点
在点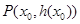 处的切线方程为
处的切线方程为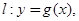 当
当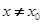 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数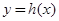 的“类对称点”,请你探究当
的“类对称点”,请你探究当 时,函数
时,函数 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
(本小题满分13分)
运货车以每小时x千米的速度匀速行驶130千米(60≤x≤100),假设汽油的价格是每升2元,而汽车每小时耗油 升,付给司机的工资是每小时14元。
升,付给司机的工资是每小时14元。
(1) 求这次行车总费用y关于x的表达式
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com