
题目列表(包括答案和解析)
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
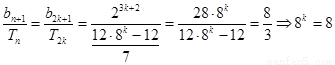
 ,
,
| 4 | x+1 |
| 4x+2 |
| x+3 |
| ax+b |
| cx+d |
| an-x1 |
| an-x2 |
| lim |
| n→∞ |
(本题满分12分)
某港口 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口 北偏西
北偏西 且与该港口相距
且与该港口相距 海里的
海里的 处,并正以
处,并正以 海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过 小时与轮船相遇。
小时与轮船相遇。

(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?XK]
(2)为保证小艇在 分钟内(含
分钟内(含 分钟)能与轮船相遇,试确定小艇航行速度的最小值;[来(
分钟)能与轮船相遇,试确定小艇航行速度的最小值;[来(
(3)是否存在 ,使得小艇以
,使得小艇以 海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定
海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com