
题目列表(包括答案和解析)
设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() .”
.”
(1)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(3)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() .
.
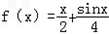 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.
D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.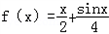 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.试用这一性质证明:方程f(x)﹣x=0只有一个实数根;
D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.试用这一性质证明:方程f(x)﹣x=0只有一个实数根;①方程f(x)-x=0有实数根;②函数f(x)的导函数f′(x)满足0<f′(x)<1.
(1)判断函数f(x)=![]() x+
x+![]() sinx是否是集合M中的元素,并说明理由;
sinx是否是集合M中的元素,并说明理由;
(2)集合M中的元素f(x)具有下列性质:
若f(x)的定义域为I,则对于任意[m,n]![]() I都存在x0∈[m,n],使得等式f(n)-f(m)=(n-m)f′(x0)成立.
I都存在x0∈[m,n],使得等式f(n)-f(m)=(n-m)f′(x0)成立.
请利用这一性质证明:方程f(x)-x=0有唯一的实数根;
(3)若存在实数x1,使得m中元素f(x)定义域中的任意实数a、b都有|a-x1|<1和|b-x1|<1成立.证明:|f(b)-f(a)|<2
集合A是由适合以下性质的函数 构成的:对于定义域内任意两个不相等的实数
构成的:对于定义域内任意两个不相等的实数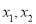 ,都有
,都有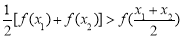 .
.
(1)试判断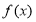 =
=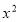 及
及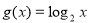 是否在集合A中,并说明理由;
是否在集合A中,并说明理由;
(2)设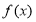 ?A且定义域为?0,??,值域为?0,1?,
?A且定义域为?0,??,值域为?0,1?,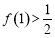 ,试写出一个满足以上条件的函数
,试写出一个满足以上条件的函数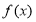 的解析式,并给予证明.
的解析式,并给予证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com