练习册

  • 练习册
  • 试题
    通过应用对数知识解决实际问题.帮助学生确立科学思想.进一步认识数学在现代生活.生产中的重要作用. 【查看更多】

     

    题目列表(包括答案和解析)

    经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(km/h)之间的函数关系为y=(v>0).

    (1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时)

    (2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?

    本题主要考查函数、不等式等基本知识,考查应用数学知识分析问题和解决问题的能力.

    查看答案和解析>>

    在函数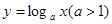的图象上有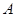、、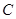三点，横坐标分别为其中．

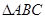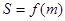    ⑴求的面积的表达式；

    ⑵求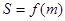的值域．

    【解析】由题意利用分割可先表示三角形ABC的面积，然后应用对数运算性质及二次函数的性质求解函数的最大值，属于知识的简单综合.

     

    查看答案和解析>>

    当兔子和狐狸处于同一栖息地时，忽略其他因素，只考虑兔子数量和狐狸数量的相互影响，为了简便起见，不妨做如下假设：
    （1）由于自然繁殖，兔子数每年增长10%，狐狸数每年减少15%；
    （2）由于狐狸吃兔子，兔子数每年减少狐狸数的0.15倍，狐狸数每年增加兔子数的0.1倍；
    （3）第n年时，兔子数量Rn用表示，狐狸数量用Fn表示；
    （4）初始时刻（即第0年），兔子数量有R0=100只，狐狸数量有F0=30只．
    请用所学知识解决如下问题：
    （1）列出兔子与狐狸的生态模型；
    （2）求出Rn、Fn关于n的关系式；
    （3）讨论当n越来越大时，兔子与狐狸的数量是否能达到一个稳定的平衡状态，说明你的理由．

    查看答案和解析>>

    对于任意向量
    a
    、
    b
    ，定义新运算“※”：
    a
    ※
    b
    =|
    a
    |•|
    b
    |•sinθ    （其中 θ为
    a
    与
    b
    所的角）．利用这个新知识解决：若|
    a
    |=1， |
    b
    |=5    ，且
    a
    •
    b
    =4    ，则
    a
    ※
    b
    =
    3
    3
    ．

    查看答案和解析>>

    某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间（单位：分钟）进行了统计，如下表．若视频率为概率，请用有关知识解决下列问题．
    病症及代号 普通病症A1 复诊病症A2 常见病症A3 疑难病症A4 特殊病症A5
    人数 100 300 200 300 100
    每人就诊时间
    （单位：分钟）    		 3 4 5 6 7
    （1）用ξ表示某病人诊断所需时间，求ξ的数学期望．并以此估计专家一上午（按3小时计算）可诊断多少人；
    （2）某病人按序号排在第三号就诊，设他等待的时间为ξ，求P（ξ≤8）；
    （3）求专家诊断完三个病人恰好用了一刻钟的概率．

    查看答案和解析>>


    同步练习册答案