（1）为了解决资金缺口，第一年初向银行贷款1 000万元，利率为5.5%（不计复利），第五年底一次性应向银行偿还本息共计多少万元？

（2）从新产品投产的第三年开始，从100万元的生产准备金中，新旧两种产品各应投入多少万元，才能使年利润最大？

（3）从新旧产品的五年总利润中最高拿出70%来，能否还清对银行的欠款？

（本小题满分12分）

已知甲、乙两个工厂在今年的1月份的利润都是6万，且乙厂在2月份的利润是8万元．若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型：f(x)＝a₁x²—4x＋6，g(x)＝a₂＋b₂(a₁，a₂，b₂∈R)．

(1)求函数f(x)与g(x)的解析式；

(2)求甲、乙两个工厂今年5月份的利润；

(3)在同一直角坐标系下画出函数f(x)与g(x)的草图，并根据草图比较今年1—10月份甲、乙两个工厂的利润的大小情况．

（本小题满分12分）
已知甲、乙两个工厂在今年的1月份的利润都是6万，且乙厂在2月份的利润是8万元．若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型：f(x)＝a₁x²—4x＋6，g(x)＝a₂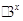＋b₂(a₁，a₂，b₂∈R)．
(1)求函数f(x)与g(x)的解析式；
(2)求甲、乙两个工厂今年5月份的利润；
(3)在同一直角坐标系下画出函数f(x)与g(x)的草图，并根据草图比较今年1—10月份甲、乙两个工厂的利润的大小情况．