题目列表(包括答案和解析)
已知函数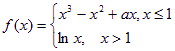
，在x=1处连续.
（I）求a的值；
（II）求函数
的单调减区间；
（III）若不等式
恒成立，求c的取值范围.
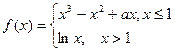，在x=1处连续.
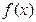的单调减区间；
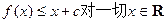恒成立，求c的取值范围. （本题满分14分）已知
，
，
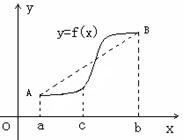
（1）若f(x)在
处取得极值，试求c的值和f(x)的单调增区间；
（2）如右图所示，若函数
的图象在
连续光滑，试猜想拉格朗日中值定理：即一定存在
使得
？（用含有a,b,f(a),f(b)的表达式直接回答）
（3）利用（2）证明：函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
，
，
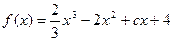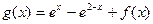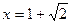处取得极值，试求c的值和f(x)的单调增区间；
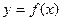的图象在
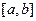连续光滑，试猜想拉格朗日中值定理：即一定存在
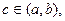使得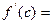
？（用含有a,b,f(a),f(b)的表达式直接回答） 已知函数
）
(1) 求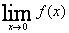
；
（2）若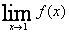
存在，求a,b的值；
（3）若函数f(x)在x=1处连续，求a,b所满足的条件；
（4）若对xÎ[0,2]，不等式f（x）<c2恒成立，求c的取值范围。
一、选择题
BDCBB DCBCB AA
二、填空题
13．300 14．（文）
（理）3 15．
16．①③④
三、解答题
17．解：（1）
，
且与向量
又
，
（2）由（1）可得A+C
，
8分
10分
，
当且仅当
时，
12分
18．（文科）解：设既会唱歌又会跳舞的有x人，则文娱队共有（7－x）人，那么只会一项的人数是（7－2x）人，
（1）
即
故文娱队共有5人。（8分）
（2）P（
=1）
（12分）
（理科）解：（1）甲得66分（正确11题）的概率为
……………………2分
乙得54分（正确9题）的概率为
………………4分
显然P1=P2，即甲得66分的概率与乙得54分的概率一样大。………………6分
（2）设答错一题倒扣x分，则学生乙选对题的个数为
随机选择20个题答对题的个数的期望为
，
得分为
，=6
令
即每答错一题应该倒扣2分。……………………12分
19．解（1）取BD中点N，连AN、MN
∵MN//BC
∴∠AMN或其邻补角就是异面直线AM与BC所成的角，在△AMN中，
（4分）
（2）取BE中点P，连AP、PM，作MQ⊥AP于Q，
过Q作QH⊥AB于H，连MH，
∵EB⊥AP，EB⊥PM
∵EB⊥面APM即EB⊥MQ，
∴MQ⊥面AEB
∴HQ为MH在面AEB上的射影，即MH⊥AB
∴∠MHQ为二面角M―AB―E的平面角，
在△AMO中，
在△ABP中，
∴二面角M―AB―E的大小，为
（8分）
（3）若将图（1）与图（2）面ACD重合，该几何体是5面体
这斜三棱柱的体积=3VA-BCD=
（12分）
20．（文科）（1）
，
即
…………………………2分
……………………4分
当
恒成立，
的单调区间为
当
…………………………6分
此时，函数
上是增函数，
在
上是减函数……………………8分
（2）
直线
的斜率为－4………………9分
假设
无实根
不可能是函数图象的切线。………………12分
（理科）（1）
由于A、B、C三点共线，
即
……………………2分
故
…………………………4分
（2）令
由
上是增函数……………………6分
故
即
………………………………8分
（3）原不等式等价于
令
………………10分
当
令
得
12分
21．解：（I）由
因直线
故所求椭圆方程为
（II）当L与x轴平行时，以AB为直径的圆的方程：
当L与y轴平行时，以AB为直径的圆 的方程：
即两圆相切于点（0，1）
因此，所求的点T如果存在，只能是（0，1）。事实上，点T（0，1）就是所求的点，证明如下。
若直线L垂直于x轴时，以AB为直径的圆过点T（0，1）
若直线L不垂直于x轴时，可设直线
由
记点
又因为
所以
，即以AB为直径的圆恒过点T（0，1），故在坐标平面上存在一个定点T（0，1）满足条件
22．（文科）解：（I）
曲线C在点
（2分）
令
依题意点
又
（4）
（5分）
（II）由已知
①
②
①-②得
（9分）
（10分）
又
又当
（13）
综上
（14分）
22．（理科）解：（I）
2
（II）
3分
4分
上是增函数 5分
又当
也是单调递增的 6分
当
此时，
不一定是增函数 7分
（III）当
当
欲证：
即证：
即需证：
猜想
………………8分
构造函数
在（0，1）上时单调递减的，
……………………10分
设
，
同理可证
成立……………………12分
分别取
，所以n-1个不等式相加即得：
……………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com