
题目列表(包括答案和解析)
在“测定滑轮组机械效率”实验中。
(1)实验所必需是器材有:铁架台、滑轮组、细线、钩码和________。
(2)求有用功应测出的物理量是________________;求总功应测出的物理量是____________。
(3)根据实验测定的物理量计算机械效率的表达式是____________________。
(4)下面的表格是两组同学实验时测得的两组平均数据,根据表中所给的数据,计算表中未知的数据,并填入表中:
| 组别 | 每个滑轮组 含滑轮个数 | 钩码重G/N | 钩码升高的高度h/m | 拉力F/N | 弹簧测力计移动的距离s/m | 机械效率
|
| 甲组 | 一个定滑轮 一个动滑轮 | 9.8 | 0.1 | 5.6 | 0.2 | |
| 乙组 | 二个定滑轮 二个动滑轮 | 9.8 | 0.1 | 2.4 |
建筑工地上,水泥板质量为0.9 t,起重机在10 s内把它匀速提升4 m的高度,若起重机的电动机所做的功为5.0×l04 J。取g=10N/kg。求:
(1)起重机的电动机的功率;
(2)起重机的机械效率。
序号 | 物理量 | 计算公式 | 备注 | |
1 | 速度 | υ= S / t | 1m / s = 3.6 Km / h 声速340m / s 光速3×108 m /s | |
2 | 温度 | t : 摄氏度(0c) | ||
3 | 密度 | ρ= m / V | 1 g / c m3 = 103 Kg / m3 | |
4 | 合力 | F = F1 - F2 F = F1 + F2 | F1、F2在同一直线线上且方向相反 F1、F2在同一直线线上且方向相同 | |
5 | 压强 | p = F / S=ρg h | p = F / S适用于固、液、气 p =ρg h适用于固体中的柱体 p =ρg h可直接计算液体压强 | |
1标准大气压 = 76 cmHg柱 = 1.01×105 Pa = 10.3 m水柱 | ||||
6 | 浮力 | ①F浮 = F上 - F下 ②F浮 = G – F ③漂浮、悬浮:F浮 = G ④F浮 = G排 =ρ液g V排 ⑤据浮沉条件判浮力大小 | 计算浮力的步骤: (1)判断物体是否受浮力 (2)根据物体浮沉条件判断物体处于什么状态 (3)找出合适的公式计算浮力 | |
物体浮沉条件(前提:物体浸没在液体中且只受浮力和重力): ①F浮>G(ρ液>ρ物)上浮至漂浮 ②F浮 =G(ρ液 =ρ物)悬浮 ③F浮 < G(ρ液 < ρ物)下沉 | ||||
7 | 杠杆平衡 | F1 L1 = F2 L 2 | 杠杆平衡条件也叫杠杆原理 | |
8 | 滑轮组 | F = G / n F =(G动 + G物)/ n S = nh (υF = nυG) | 理想滑轮组 忽略轮轴间的摩擦 n:作用在动滑轮上绳子股数 | |
9 | 斜面公式 | F L = G h | 适用于光滑斜面 | |
10 | 功 | W = F S = P t | 1J = 1N·m = 1W·s | |
11 | 功率 | P = W / t = Fυ | 1KW = 103 W,1MW = 103KW | |
12 | 有用功 | W有用 = G h(竖直提升)= F S(水平移动)= W总 – W额 =ηW总 | ||
13 | 额外功 | W额 = W总 – W有 = G动 h(忽略轮轴间摩擦)= f L(斜面) | ||
14 | 总功 | W总= W有用+ W额 = F S = W有用 / η | ||
15 | 机械效率 | η= W有用 / W总=G /(n F) = G物 /(G物 + G动) | 定义式 适用于动滑轮、滑轮组 | |
16 | 热量 | Q=Cm△t Q=qm | ||
17 | 欧姆定律 | I=U/R | 适用于纯电阻电路 | |
18 | 焦耳定律 | Q=I2Rt | 适用于所有电路的电热计算 | |
19 | 电功 | 定义式—W=UIt=Pt(普适) 导出式—W=I2Rt;(串) W=(U2/R)t;(并) | (1)使用公式时,各物理量通常都采用国际单位。 (2)对于物理量的定义式还需其物理意义。 (3)注意公式的适用范围 (4)会灵活对基本公式进行变形 | |
20 | 电功率 | 定义式——P=W/ t=UI (普适) 导出式——P=I2R;(串) P=U2/R;(并) | ||
21 | 串联电路 | I=I1=I2 U=U1+U2 R=R1+R2 | ||
22 | 并联电路 | I=I1+I2 U=U1=U2 1/R=1/R1+1/R2 | R=R1R2 /(R1+R2) | |
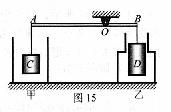
如图15所示,有两个底面积均为S的实心圆柱体C和D,分别用两根细绳的一端系于它们的上表面的中央,细绳的另一端分别系在轻质杠杆的两端,杠杆恰好水平平衡。把质量为800g的酒精缓慢注入底面积为S![]() 的圆柱形容器甲中,同时向上下横截面积分别为S
的圆柱形容器甲中,同时向上下横截面积分别为S![]() 、S
、S![]() 的圆柱形容器乙中注入某种液体,当两容器中液体均静止,且杠杆再次水平平衡时,圆柱体C下底浸入酒精中的深度为2.5cm,酒精对容器甲底面的压强为1100Pa,圆柱体D下底浸入液体的深度为4cm。若把圆柱体D从B端取下后将其从原位置再竖直向下移动2.5 cm,圆柱体D刚好被液体浸没,此时细线的拉力为10.5N。在圆柱体D向下移动过程中,液体在容器乙截面积不同的上、下两部分上升的体积相等,在以上整个操作过程中,两容器中液体均未溢出,且圆柱体C和D均未与容器壁接触。已知酒精的密度为0.8×10
的圆柱形容器乙中注入某种液体,当两容器中液体均静止,且杠杆再次水平平衡时,圆柱体C下底浸入酒精中的深度为2.5cm,酒精对容器甲底面的压强为1100Pa,圆柱体D下底浸入液体的深度为4cm。若把圆柱体D从B端取下后将其从原位置再竖直向下移动2.5 cm,圆柱体D刚好被液体浸没,此时细线的拉力为10.5N。在圆柱体D向下移动过程中,液体在容器乙截面积不同的上、下两部分上升的体积相等,在以上整个操作过程中,两容器中液体均未溢出,且圆柱体C和D均未与容器壁接触。已知酒精的密度为0.8×10![]() kg/m
kg/m![]() ,S
,S![]() 为80cm
为80cm![]() ,AO:OB=3:1,S
,AO:OB=3:1,S![]() :S=5:4,S
:S=5:4,S![]() :S=9:4,g取10N/kg,则圆柱体D的密度为_____kg/m
:S=9:4,g取10N/kg,则圆柱体D的密度为_____kg/m![]() 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com