
题目列表(包括答案和解析)
 的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,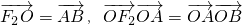
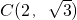 ,求双曲线的方程;
,求双曲线的方程;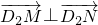 ,求直线l的方程.
,求直线l的方程. 的离心率e=2,F1,F2是左,右焦点,过F2作x轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知
的离心率e=2,F1,F2是左,右焦点,过F2作x轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知
 的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
 ,求双曲线的方程;
,求双曲线的方程;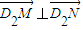 ,求直线l的方程.
,求直线l的方程.双曲线![]() -
-![]() =1(a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线上任一点,F2在∠F1PF2的内角平分线上的射影为M,则点M的轨迹是以原点为圆心,半径为a的圆.类比到椭圆中,写出类似的性质并加以证明.
=1(a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线上任一点,F2在∠F1PF2的内角平分线上的射影为M,则点M的轨迹是以原点为圆心,半径为a的圆.类比到椭圆中,写出类似的性质并加以证明.
(14分)设F1、F2分别为椭圆C: =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1, )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
(吉林、黑龙江、广西)
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
A
B
C
C
A
D
A
C
B
C
二、填空
13 (x-1)2+(y-2)2=4; 14、- ; 15、 384;16、①②③④
三、解答题:
17、本小题主要考查指数函数的性质、不等式性质和解法,考查分析问题的能力和运算能力
解:∵f (x)=2|x+1|-|x-1|≥2=, 即|x+1|-|x-1|≥.
当x≤ -1时,原不等式化为:-2≥(舍);
当-1<x≤ 1时,原不等式化为:2x≥ ∴x≥.
∴此时,≤ x≤ 1;
当x>1时, 原不等式化为:2≥,
此时,x>1.
故原不等式的解集为:{x|x≥ }.
18、本小题主要考查等差数列、等比数列的基本知识以及运用这些知识的能力
⑴证明:设{an}中首项为a1,公差为d.
∵lga1,lga2,lga4成等差数列 ∴2lga2=lga1?lga4 ∴a22=a1?a4.
即(a1+d)2=a1(a1+3d) ∴d=0或d=a1.
当d=0时, an=a1, bn=, ∴,∴为等比数列;
当d=a1时, an=na1 ,bn=,∴,∴为等比数列.
综上可知为等比数列.
⑵∵无穷等比数列{bn }各项的和
∴|q|<1, 由⑴知,q=, d=a1 . bn=
∴, ∴a1=3.
∴.
19、本小题考查离散型随机变量分布列和数学期望等概念,考查运用概率知识解决实际问题的能力
解:ξ的所有取值为3,4,5
P(ξ=3)=;
P(ξ=4)=;
P(ξ=5)=.
ξ
3
4
5
P
0.28
0.3744
0.3466
∴ξ的分布列为:
∴Eξ=3×0.28+4×0.3744+5×0.3456=0.84+1.4976+1.728=4.0656.
20、本小题主要考查直线与平面垂直、直线与平面所成角的有关知识、及思维能力和空间想象能力,考查应用向量知识解决数学问题的能力
解:方法一:
⑴取PA中点G, 连结FG, DG.
.
⑵设AC, BD交于O,连结FO.
.
设BC=a, 则AB=a, ∴PA=a, DG=a=EF, ∴PB=2a, AF=a.
设C到平面AEF的距离为h.
∵VC-AEF=VF-ACE, ∴. 即 ∴. ∴AC与平面AEF所成角的正弦值为.
即AC与平面AEF所成角为.
21、本小题主要考查椭圆和直线的方程与性质,两条直线垂直的条件、两点间的距离、不等式的性质等基本知识及综合分析能力
解:∵. 即.
当MN或PQ中有一条直线垂直于x轴时,另一条直线必垂直于y轴. 不妨设MN⊥y轴,则PQ⊥x轴.
∵F(0, 1) ∴MN的方程为:y=1,PQ的方程为:x=0分别代入椭圆中得:|MN|=, |PQ|=2.
∴S四边形PMQN=|MN|?|PQ|=××2=2.
当MN,PQ都不与坐标轴垂直时,设MN的方程为y=kx+1 (k≠0),代入椭圆中得:(k2+2)x2+2kx-1=0, ∴x1+x2=, x1?x2=.
∴
同理可得:.
∴S四边形PMQN=|MN|?|PQ|==
(当且仅当即时,取等号).
又S四边形PMQN =,∴此时, S四边形PMQN.
综上可知:(S四边形PMQN )max=2, (S四边形PMQN )min=.
22、本小题主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力
解:⑴令=0 即[x2-2(a-1)x-2a]ex=0 ∴x2-2(a-1)x-2a=0
∵△=[2(a-1)]2+8a=4(a2+1)>0 ∴x1=, x2=
又∵当x∈(-∞, )时,>0;
当x∈(, )时,<0;
当x∈(, +∞)时,>0.
∴x1, x2分别为f (x)的极大值与极小值点.
又∵;当时.
而f ()=<0.
∴当x=时,f (x)取得最小值.
⑵f (x)在[-1, 1]上单调,则≥ 0(或≤ 0)在[-1, 1]上恒成立.
而=[x2-2(a-1)x-2a]ex, 令g(x)= x2-2(a-1)x-2a=[x-(a-1)]2-(a2+1).
∴≥ 0(或≤ 0) 即g(x) ≥ 0(或≤ 0).
当g(x) ≥ 0在[-1, 1]上恒成立时有:
①当-1≤ a-1 ≤1即0≤ a ≤2时, g(x)min=g(a-1)= -(a2+1) ≥ 0(舍);
②当a-1>1即a ≥ 2时, g(x)min=g(1)= 3-4a ≥ 0 ∴a≤(舍).
当g(x) ≤ 0在[-1, 1]上恒成立时,有:
①当-1≤ a-1 ≤ 0即0≤ a ≤ 1时, g(x)max=g(1)=3-4a ≤ 0, ∴≤ a ≤ 1;
②当0< a-1 ≤ 1即1< a ≤ 2时, g(x)max=g(-1)= -1 ≤ 0, ∴1< a ≤ 2;
③当1< a-1即a > 2时, g(x)max=g(-1)= -1 ≤ 0, ∴a >2.
故a∈[,+∞].
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com