练习册

  • 练习册
  • 试题
    例如.做1000次试验.即N=1000.模拟得到N1=689.所以=0.689.即S0.689．Excll操作步骤:S1:分别在单元格A1,B1,C1中键入a,b,b-1/(a+1)S2:在A2单元格中插入函数/RAND/确定/确定/拖动单元格到A10001生成1000个随机数S3:同S2在单元格B列也生成一系列1000个随机数S4:在C列计算b-1/(a+1)的每个值S5:在D列任意一个单元格.用countif函数统计C列小于0的数字个数S6:S5中得到的数除以1000.得到该值的近似数就是面积 【查看更多】

     

    题目列表(包括答案和解析)

    利用计算机随机模拟方法计算图中阴影面积（如图所示）
    第一步：利用计算机产生两个0～1区间的均匀随机数，x，y，其中-1＜x＜1，0＜y＜1；
    第二步：拟（x，y）为点的坐标．共做此实验N次．若落在阴影部分的点的个数为N1，
    则可以计算阴影部分的面积S．例如：做了2000次实验，即N=2000，模拟得到N1=1396，所以S=
    1.396
    1.396
    ．

    查看答案和解析>>

    设甲、乙、丙三人每次射击命中目标的概率分别为
    1
    4
    、
    1
    3
    、
    1
    2
    ．
    （1）若三人各向目标射击一次，求至少有一人命中目标的概率；
    （2）若甲单独向目标连续射击三次，求他恰好命中两次的概率；
    （3）若甲向目标连续射击1000次，试估计他命中目标的次数．

    查看答案和解析>>

    18、做重复实验：抛掷同一枚啤酒瓶盖1000次．经过统计得“凸面向上”的频率约为0.44，则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为

    查看答案和解析>>

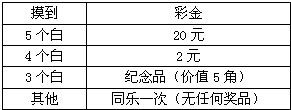    精英家教网有一个摆地摊的赌主，他拿了8个白的，8个黑的围棋子，放在1个签袋里，他规定：凡愿摸彩者，每人交1元钱作“手续费”，然后一次从袋里摸出5个棋子，中奖情况如下表：
    试计算（1）能获得20元彩金的概率；
    （2）按摸1000次统计，赌主可净赚多少？

    查看答案和解析>>

    摆地摊的某摊（赌）主拿了8个白的，8个黑的围棋子放在一个口袋里，并规定凡愿意摸彩者每人交一元钱作手续费，然后一次从口袋摸出5个棋子，中彩情况如下：

    摸棋子

    5个白

    4个白

    3个白

    其它

    彩金

    20元

    2元

    纪念品（价值5角）

    同乐一次（无任何奖品）

           试计算：

           （1）获得20元彩金的概率；

           （2）获得2元彩金的概率；

           （3）获得纪念品的概率；

           （4）按摸彩1000次统计，赌主可望净赚多少钱？

    查看答案和解析>>


    同步练习册答案