
题目列表(包括答案和解析)
| k | x |
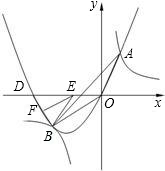 的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点). 图象相交于点A,B,已知点A
图象相交于点A,B,已知点A 的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点). 图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
 图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
 图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).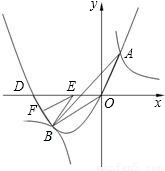
一、选择题
1、 ; 2、
; 2、 ; 3、
; 3、 ; 4、
; 4、 ; 5、
; 5、 ; 6、
; 6、 .
.
二、填空题
7、5;
8、 ;
9、
;
9、 ;
10、
;
10、 ;
;
11、 ;
12、
;
12、 ;
13、
;
13、 >
> ;
14、
;
14、 ;
;
15、 ;
16、
;
16、 ;
17、120;
18、8.
;
17、120;
18、8.
三、解答题
19、解:原式 ――――――――――――――(2+2+1=5分)
――――――――――――――(2+2+1=5分)
 ――――――――――――――――――――(2分)
――――――――――――――――――――(2分)
 ――――――――――――――――――――――――(2分)
――――――――――――――――――――――――(2分)
 .―――――――――――――――――――――――――(1分)
.―――――――――――――――――――――――――(1分)
20、解:(1)由点 在反比例函数图像上,则
在反比例函数图像上,则 ,―――――――――(1分)
,―――――――――(1分)
又点 与
与 在一次函数图像上,
在一次函数图像上,
则 ,―――――――――――――――――――――(2分)
,―――――――――――――――――――――(2分)
解得 .―――――――――――――――――――――――(1分)
.―――――――――――――――――――――――(1分)
∴一次函数解析式为 .―――――――――――――――(1分)
.―――――――――――――――(1分)
(2)由 ,―――――――――――――――――――――(2分)
,―――――――――――――――――――――(2分)
消元得 ,―――――――――――――――――(1分)
,―――――――――――――――――(1分)
解得 (舍去),――――――――――――――(1分)
(舍去),――――――――――――――(1分)
∴点 的坐标是
的坐标是 .――――――――――――――――(1分)
.――――――――――――――――(1分)
21、解:(1)令 ,
,
由菱形 得
得 ,――――――――――――――(1分)
,――――――――――――――(1分)
则在 中,
中, ,――――――――(2分)
,――――――――(2分)
∴ .――――――――――――――――――(2分)
.――――――――――――――――――(2分)
(2)∵ ,
,
∴ .――――――――――――――――――――――――(1分)
.――――――――――――――――――――――――(1分)
又在 中,
中, .――――――――(2分)
.――――――――(2分)
∵ ,
,
∴ .――――――――――――――――――――――――(2分)
.――――――――――――――――――――――――(2分)
22、解:(1)图略;―――――――――――――――――――――――――――(3分)
(2)200×12%=24(户).――――――――――――――――――――(2分)
答:回答“非常满意”的居民有24户.――――――――――――――――(1分)
(3) (户).――――――――――――――(2+1=3分)
(户).――――――――――――――(2+1=3分)
答:对“违章搭建情况”不满意或非常不满意的居民估计有1854户.―――(1分)
23、解:(1)∵ ,
,
∴ ,
,
∴ .―――――――――――――――――――――――(2分)
.―――――――――――――――――――――――(2分)
∵ ,
,
∴ ≌
≌ ,――――――――――――――――――――(3分)
,――――――――――――――――――――(3分)
∴ .――――――――――――――――――――(1分)
.――――――――――――――――――――(1分)
(2)答: .――――――――――――――――――――――(1分)
.――――――――――――――――――――――(1分)
∵ ,
,
∴
∵ ,
,
∴ ,
,
∴ ―――――――――――――――――――――――(2分)
―――――――――――――――――――――――(2分)
∵ ,
, ,
,
∴ ≌
≌ ,――――――――――――――――――――(1分)
,――――――――――――――――――――(1分)
∴ .
.
∵ ,―――――――――――――――――――――――(1分)
,―――――――――――――――――――――――(1分)
∴ .―――――――――――――――――――――――(1分)
.―――――――――――――――――――――――(1分)
24、解:(1)∵点 与
与 在二次函数图像上,
在二次函数图像上,
∴ ,――――――――――――――――――(2分)
,――――――――――――――――――(2分)
解得 ,――――――――――――――――――――――(1分)
,――――――――――――――――――――――(1分)
∴二次函数解析式为 .――――――――――(1分)
.――――――――――(1分)
(2)过 作
作 轴于点
轴于点 ,由(1)得
,由(1)得 ,――――――――(1分)
,――――――――(1分)
则在 中,
中, ,
,
又在 中,
中, ,―――――――(1分)
,―――――――(1分)
∵ ,――――――――――――――――(1分)
,――――――――――――――――(1分)
∴ .―――――――――――――――――――(1分)
.―――――――――――――――――――(1分)
(3)由 与
与 ,可得直线
,可得直线 的解析式为
的解析式为 ,―(1分)
,―(1分)
设 ,
,
则 ,
,
∴ .
.
∴ .――――――――――――――(1分)
.――――――――――――――(1分)
当 ,
,
解得  (舍去),
(舍去),
∴ .――――――――――――――――――――――(1分)
.――――――――――――――――――――――(1分)
当 ,
,
解得  (舍去),
(舍去),
∴ .――――――――――――――――――――――(1分)
.――――――――――――――――――――――(1分)
综上所述,存在满足条件的点,它们是 与
与 .
.
25、解:(1)过 作
作 于
于 ,
,
∵ ,
,
∴ .
.
则在 中,
中, ,―――――――――(2分)
,―――――――――(2分)
∴ .――――――――――――――――(1分)
.――――――――――――――――(1分)
(2)令此时正方形的边长为 ,
,
则 ,―――――――――――――――――――――――(2分)
,―――――――――――――――――――――――(2分)
解得 .――――――――――――――――――――――――(1分)
.――――――――――――――――――――――――(1分)
(3)当 时,――――――――――――――――――――――(1分)
时,――――――――――――――――――――――(1分)
 .―――――――――――――――――――(1分)
.―――――――――――――――――――(1分)
当 时,――――――――――――――――――――――(1分)
时,――――――――――――――――――――――(1分)
 .――――――――――――――(2分)
.――――――――――――――(2分)
(4) .――――――――――――――――(1+1+1=3分)
.――――――――――――――――(1+1+1=3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com