
题目列表(包括答案和解析)
(本小题满分12分)如下图,某隧道设计为双向四车道,车道总宽20 m,要求通行车辆限高5 m,隧道全长2.5 km,隧道的两侧是与地面垂直的墙,高度为3米,隧道上部拱线近似地看成半个椭圆.


(1)若最大拱高h为6 m,则隧道设计的拱宽l是多少?
(2)若要使隧道上方半椭圆部分的土方工程量最小,则应如何设计拱高h和拱宽l?
(已知:椭圆![]() +
+![]() =1的面积公式为S=
=1的面积公式为S=![]() ,柱体体积为底面积乘以高.)
,柱体体积为底面积乘以高.)
(3)为了使隧道内部美观,要求在拱线上找两个点M、N,使它们所在位置的高度恰好是限高5m,现以M、N以及椭圆的左、右顶点为支点,用合金钢板把隧道拱线部分连接封闭,形成一个梯形,若l=30m,梯形两腰所在侧面单位面积的钢板造价是梯形顶部单位面积钢板造价的![]() 倍,试确定M、N的位置以及
倍,试确定M、N的位置以及![]() 的值,使总造价最少.
的值,使总造价最少.
(本小题满分12分)已知函数![]() 处的切线恰好为
处的切线恰好为![]() 轴。 (I)求
轴。 (I)求![]() 的值;(II)若区间
的值;(II)若区间![]() 恒为函数
恒为函数![]() 的一个单调区间,求实数
的一个单调区间,求实数![]() 的最小值;(III)记
的最小值;(III)记![]() (其中
(其中![]() ),
),![]() 的导函数,则函数
的导函数,则函数![]() 是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。
是否存在极值点?若存在,请找出极值点并论证是极大值点还是极小值点;若不存在,请说明理由。
 (本小题满分12分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(本小题满分12分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(I)设![]() (单位:米),要使花坛AMPN的面积大于32平方米,求
(单位:米),要使花坛AMPN的面积大于32平方米,求![]() 的取值范围;
的取值范围;
(II)若![]() (单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(本小题满分12分)自然状态下的鱼类是一种可再生的资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用 表示某鱼群在第
表示某鱼群在第 年初的总量,
年初的总量, ,且
,且 。不考虑其他因素,设在第
。不考虑其他因素,设在第 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与 成正比,死亡量与
成正比,死亡量与 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数 其中
其中 称为捕捞强度。
称为捕捞强度。
(1)求 与
与 的关系式;
的关系式;
(2)设 ,为了保证对任
,为了保证对任 意
意 ,都有
,都有 ,则捕捞强度
,则捕捞强度 的最大允许值是多少?证明你的结论。
的最大允许值是多少?证明你的结论。
(本小题满分12分)有这样一则公益广告:“人们在享受汽车 带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于
带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于 年起取消
年起取消 排放量超过
排放量超过 的
的 型新车挂牌.检测单位对目前该市保有量最大的甲类
型新车挂牌.检测单位对目前该市保有量最大的甲类 型品牌车随机抽取
型品牌车随机抽取 辆进行了
辆进行了 排放量检测,
排放量检测, 记录如下(单位:
记录如下(单位: ).
).
(Ⅰ)已知 ,求
,求 的值及样本标准差;
的值及样本标准差;
(Ⅱ)从被检测的甲类品牌车中任取2辆,则至少有一辆不符合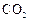 排放量的概率是多少?
排放量的概率是多少?
一、选择题
(1)B (2)C (3)A (4)D (5)D (6)B
(7)A (8)D (9)B (10)C (11)A (12) B
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)28 (14).files\image074.png) (15)
(15).files\image047.png) (16)2
(16)2
三、解答题
(17)本小题主要考查同角三角函数的基本关系式,二倍角公式以及三角函数式的恒等变形等基础知识和基本技能.满分12分.
解:.files\image132.png)
.files\image134.png)
当.files\image136.png) 为第二象限角,且
为第二象限角,且.files\image138.png) 时
时
.files\image140.png) ,
,
所以.files\image098.png) =
=.files\image142.png)
(18)本小题主要考查等比数列的概念、前n项和公式等基础知识,考查学生综合运用基础知识进行运算的能力.满分12分.
解:(I)设等比数列{an}的公比为q,则a2=a1q, a5=a1q4.
.files\image143.png) a1q=6,
a1q=6,
依题意,得方程组 a1q4=162.
解此方程组,得a1=2, q=3.
故数列{an}的通项公式为an=2?3n-1.
(II) .files\image145.png)
.files\image147.png)
(19)本小题主要考查导数的几何意义,两条直线垂直的性质以及分析问题和综合运算能力.满分12分.
解:y′=2x+1.
直线l1的方程为y=3x-3.
设直线l2过曲线y=x2+x-2上 的点B(b, b2+b-2),则l2的方程为y=(2b+1)x-b2-2
因为l1⊥l2,则有2b+1=.files\image149.png)
所以直线l2的方程为.files\image151.png)
(II)解方程组.files\image153.png) 得
得.files\image155.png)
所以直线l1和l2的交点的坐标为.files\image157.png)
l1、l2与x轴交点的坐标分别为(1,0)、.files\image159.png) .
.
所以所求三角形的面积 .files\image161.png)
(20)本小题主要考查相互独立事件同时发生的概率和互斥事件有一个发生的概率的计算方法,应用概率知识解决实际问题的能力.满分12分.
解:记“这名同学答对第i个问题”为事件.files\image163.png) ,则
,则
P(A1)=0.8,P(A2)=0.7,P(A3)=0.6.
(Ⅰ)这名同学得300分的概率
P1=P(A1.files\image165.png) A3)+P(
A3)+P(.files\image167.png) A2A3)
A2A3)
=P(A1)P(.files\image165.png) )P(A3)+P(
)P(A3)+P(.files\image167.png) )P(A2)P(A3)
)P(A2)P(A3)
=0.8×0.3×0.6+0.2×0.7×0.6
=0.228.
(Ⅱ)这名同学至少得300分的概率
P2=P1+P(A1A2A3)
=0.228+P(A1)P(A2)P(A3)
=0.228+0.8×0.7×0.6
=0.564.
(21)本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析
|