
题目列表(包括答案和解析)
| Tn+1 |
| Tn |
| Tn |
| Tn+1 |
| 1 |
| an•an+1 |
| 1 |
| 2 |
| b1+1 |
| b1 |
| b2+1 |
| b2 |
| bn+1 |
| bn |
| n+1 |
等比数列![]() 中,
中,![]() 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且![]() 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足 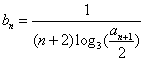 ,记数列
,记数列![]() 的前n项和为
的前n项和为![]() ,证明
,证明![]()
等比数列{![]() }的前n项和为
}的前n项和为![]() , 已知对任意的
, 已知对任意的![]() ,点
,点![]() ,均在函数
,均在函数![]() 且
且![]() 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记 ![]() 用数学归纳法证明:对任意的
用数学归纳法证明:对任意的![]() ,
,
不等式![]() 成立
成立
一、选择题
(1)D (2)C (3)A (4)D (5)A (6)B
(7)C (8)A (9)B (10)A (11)B (12)C
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)28 (14).files\image148.png) (15)
(15).files\image150.png) (16)2
(16)2
三、解答题
(17)本小题主要考查同角三角函数的基本关系式,二倍角公式以及三角函数式的恒等变形等基础知识和基本技能.满分12分.
解:.files\image152.png)
.files\image154.png)
当.files\image055.png) 为第二象限角,且
为第二象限角,且.files\image156.png) 时
时
.files\image158.png) ,
,
所以.files\image119.png) =
=.files\image160.png)
(18)本小题主要考查函数的导数计算,利用导数讨论函数的性质,判断函数的最大值、最小值以及综合运算能力.满分12分.
解:.files\image162.png)
令 .files\image164.png)
化简为.files\image166.png) 解得
解得.files\image168.png)
当.files\image170.png) 单调增加;
单调增加;
当.files\image172.png) 单调减少.
单调减少.
所以.files\image174.png) 为函数
为函数.files\image176.png) 的极大值.
的极大值.
又因为 .files\image178.png)
所以 .files\image180.png) 为函数
为函数.files\image176.png) 在[0,2]上的最小值,
在[0,2]上的最小值,.files\image174.png) 为函数
为函数.files\image176.png)
在[0,2]上的最大值.
(19)本小题主要考查离散型随机变量的分布列、数学期望等概念,以及运用概率统计知识解决实际问题的能力.满分12分.
解:(Ⅰ).files\image123.png) 的可能值为-300,-100,100,300.
的可能值为-300,-100,100,300.
P(.files\image123.png) =-300)=0.23=0.008,
P(
=-300)=0.23=0.008,
P(.files\image123.png) =-100)=3×0.22×0.8=0.096,
=-100)=3×0.22×0.8=0.096,
P(.files\image123.png) =100)=3×0.2×0.82=0.384,
P(
=100)=3×0.2×0.82=0.384,
P(.files\image123.png) =300)=0.83=0.512,
=300)=0.83=0.512,
所以.files\image123.png) 的概率分布为
的概率分布为
.files\image183.png)
-300
-100
100
300
P
0.008
0.096
0.384
0.512
根据.files\image123.png) 的概率分布,可得
的概率分布,可得.files\image123.png) 的期望
的期望
E.files\image123.png) =(-300)×0.08+(-100)×0.096+100×0.384+300×0.512=180.
=(-300)×0.08+(-100)×0.096+100×0.384+300×0.512=180.
(Ⅱ)这名同学总得分不为负分的概率为P(.files\image123.png) ≥0)=0.384+0.512=0.896.
≥0)=0.384+0.512=0.896.
|