练习册

  • 练习册
  • 试题
    (II)已知直线l的方向向量为与椭圆M交于B.C两点.求△ABC面积的最大值. 【查看更多】

     

    题目列表(包括答案和解析)

    已知双曲线
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的右顶点为A（2，0），一条渐近线为y=
    1
    2
    x    ，过点B（0，2）且斜率为k的直线l与该双曲线交于不同的两点P，Q．
    （I）求双曲线的方程及k的取值范围；
    （II）是否存在常数k，使得向量
    OP
    +
    OQ
    与
    AB
    垂直？如果存在，求k的值；如果不存在，请说明理由．

    查看答案和解析>>

    已知双曲线
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的右顶点为A（2，0），一条渐近线为y=
    1
    2
    x    ，过点B（0，2）且斜率为k的直线l与该双曲线交于不同的两点P，Q．
    （I）求双曲线的方程及k的取值范围；
    （II）是否存在常数k，使得向量
    OP
    +
    OQ
    与
    AB
    垂直？如果存在，求k的值；如果不存在，请说明理由．

    查看答案和解析>>

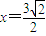    已知曲线C上任意一点到直线的距离与它到点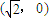的距离之比是．   
    （I）求曲线C的方程；
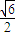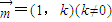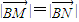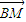    （II）设B为曲线C与y轴负半轴的交点，问：是否存在方向向量为的直线l，l与曲线C相交于M、N两点，使，且与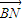夹角为60°？若存在，求出k值，并写出直线l的方程；若不存在，请说明理由．

    查看答案和解析>>

    已知双曲线数学公式的右顶点为A（2，0），右焦点为F、O为坐标原点，点F，A到渐近线的距离之比为数学公式，过点B（0，2）且斜率为k的直线l与该双曲线交于不同的两点P，Q．
    （I）求双曲线的方程及k的取值范围；
    （II）是否存在常数k，使得向量数学公式垂直？如果存在，求k的值；如果不存在，请说明理由．

    查看答案和解析>>

    已知椭圆C的中心在原点，左焦点为(-
    		3
    ，0)    ，离心率为
    		3
    2
    ．设直线l与椭圆C有且只有一个公共点P，记点P在第一象限时直线l与x轴、y轴的交点分别为A、B，且向量
    OM
    =
    OA
    +
    OB
    ．
    求：
    （I）椭圆C的方程；
    （II）|
    OM
    |    的最小值及此时直线l的方程．

    查看答案和解析>>

                                      （一）

    一、选择题

    1~8：CAAD    BBBD

    二、填空题

    9、            10、35            11、           12、       

    13、          14、10            15、

    三、解答题

    16、解：（1）由及正弦定理有：    

    ∴或                                       ……….2分

    若，且，

    ∴，；                             ……….4分

    ∴，则，∴三角形．            ……….6分

    （2）∵ ，∴，

    ∴，而，               ……….8分

    ∴，∴，∴．           ……….12分

    17解：（１）取的中点的中点连结

    平面, .

    又,

    平面．……………………………3分

    ,四边形是平行四边形, 平面

    又平面, 平面平面　………………………………6分

     　（２）过作于，连结．

    由（１）中的平面平面知面，所以在面上的射影为，所以就是所求的角．  …………………………………………9分

    令正方体的棱长为，所以，所以．

    即与平面所成角的大小的正弦值为．   …………………………12分

    18解：（１）表示取出的三个球中数字最大者为3．

    ①三次取球均出现最大数字为3的概率

    ②三取取球中有2次出现最大数字3的概率

    ③三次取球中仅有1次出现最大数字3的概率

    ∴．   ……………………………………………………7分

    （２）在时, 利用（１）的原理可知：

    ,(=1,2,3,4)

    １

    ２

    ３

    ４

     的概率分布为：

     

     

    =1×＋2×＋3×＋4× = ．………………………………………………7分

    19、解：（I）由已知抛物线的焦点为

    故所求椭圆方程为                                              …………6分

       （II）设直线BC的方程为

    代入椭圆方程并化简得                …………9分

    又点A到BC的距离为，                                           …………11分

    所以△ABC面积的最大值为                                             …………14分

    20解：（１），

    设

    为增，

    当

    ，

    所以图象上的点总在图象的上方．    …………………………6分

    （２）当．

    x

    （－∞，0）

    （0，1）

    1

    （1，+∞）

    F‘（x）

    －

    －

    0

    +

    F（x）

    减

    减

    e

    增

    ①当x＞0时，F（x）在x=1时有最小值e，．

    ②当x＜0时，F（x）为减函数，

    ，

    ．

    ③当x=0时，∈R．

    由①②③，恒成立的的范围是． ……………………………………14分

    21解：（１）由得

    ．

    而，所以，

    所以数列为等比数列．    …………………………………………4分

    　 （２）由（１）有． ……………………………………6分

    所以，，……，

    ，累和得

    ． …8分

    因为，………………………………………………9分

    所以．

    记，用错位相减法得

    ，所以．

    所以．

    即当为奇数时命题成立．……………………………………………………………11分

    又，

    所以．即当为偶数时命题成立．

    综合以上得．………………………………………………13分

     

     


    同步练习册答案