
题目列表(包括答案和解析)
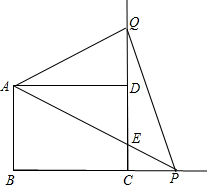 (2012•西湖区一模)如图,在矩形ABCD中,AB=3,BC=4,P是边BC延长线上的一点,连接AP交边CD于点E,把射线AP沿直线AD翻折,交射线CD于点Q,设CP=x,DQ=y,
(2012•西湖区一模)如图,在矩形ABCD中,AB=3,BC=4,P是边BC延长线上的一点,连接AP交边CD于点E,把射线AP沿直线AD翻折,交射线CD于点Q,设CP=x,DQ=y, 题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2? 解:设矩形蔬菜种植区域的宽为xm,则长为2xm,  根据题意,得x•2x=288. 解这个方程,得x1=-12(不合题意,舍去),x2=12 所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m) 答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确! 小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?. 结果为何正确呢?  (1)请指出小明解答中存在的问题,并补充缺少的过程: 变化一下会怎样… (2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由. 如图(1),在Rt△ABC中,∠B=90°,AE平分∠BAC,将AB沿AE折叠,使点B落在AC上一点D处,已知AB=6,BC=8,可用下面的方法求线段BE的长: 由折叠可知:AD=AB=6,BE=DE,∠ADE=∠ABE=90° 在Rt△ABC中,∠B=90°,∴AC2=AB2+BC2=62+82=100 ∴AC=10,CD=AC-AD=4,设BE=DE=x,则CE=8-x 在Rt△CED中,∠EDC=90°,∴EC2=ED2+CD2,即(8-x)2=x2+42,整理得:64-16x=16 解得:x=3 仿上面的解答法解答下题: 如图(2),在矩形ABCD中,AB=5cm,AD=13cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,求DE的长度. 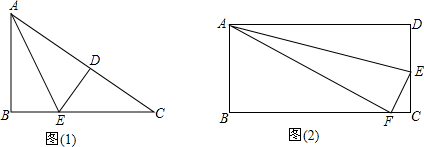 如图(1),在Rt△ABC中,∠B=90°,AE平分∠BAC,将AB沿AE折叠,使点B落在AC上一点D处,已知AB=6,BC=8,可用下面的方法求线段BE的长: |