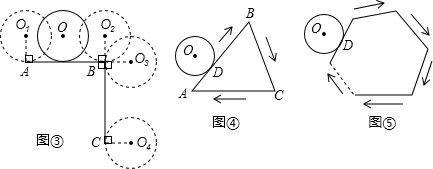
如图①至图④,半径为1的⊙O均无滑动滚动,⊙O
1、⊙O
2、⊙O
3、⊙O
4均表示⊙O与线段AB或BC相切于端点时刻的位置.
【阅读理解】

(1)如图①,⊙O从⊙O
1的位置出发,沿AB滚动到⊙O
2的位置,当AB=2π时,圆心O经过的路径长为2π.
(2)如图②,∠ABC相邻的补角∠CBA=n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O
1的位置旋转到⊙O
2的位置,⊙O绕B点旋转的角∠O
1BO
2=n°,此时,圆心O经过的路径弧O
1O
2的长为
.
【实践应用】
(1)在阅读理解(1)中,若AB=π时,则圆心O经过的路径长为
π
π
;在阅读理解(2)中,若∠ABC=120°时,则圆心O经过的路径弧O
1O
2的长为
.
(2)如图③,∠ABC=90°,AB=BC=π.⊙O从⊙O
1的位置出发,⊙O在∠ABC外部沿A-B-C滚动到⊙O
4的位置,在这个过程中,圆心O经过的路径长为
.
【拓展联想】
(1)如图④,△ABC的周长为4π,⊙O从与AB相切于点D的位置出发,在△AABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,在这个过程中,圆心O经过的路径长为
6π
6π
.
(2)如图⑤,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,在这个过程中,圆心O经过的路径长为
l+2π
l+2π
.

 如图,某人从山脚下沿着坡度i=1:
如图,某人从山脚下沿着坡度i=1: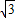 的山坡向山顶走了1000米,则他在竖直方向上升 米.
的山坡向山顶走了1000米,则他在竖直方向上升 米.
![]() 的山坡向山顶走了1000米,则他在竖直方向上升 米.
的山坡向山顶走了1000米,则他在竖直方向上升 米.
 如图,某人从山脚下沿着坡度i=1:
如图,某人从山脚下沿着坡度i=1: 的山坡向山顶走了1000米,则他在竖直方向上升________米.
的山坡向山顶走了1000米,则他在竖直方向上升________米.
