
题目列表(包括答案和解析)
 (2013•湛江)阅读下面的材料,先完成阅读填空,再按要求答题:
(2013•湛江)阅读下面的材料,先完成阅读填空,再按要求答题:| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
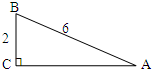 如图,∠A的正弦与余弦值分别为( )
如图,∠A的正弦与余弦值分别为( )阅读下面的材料,先完成阅读填空,再将要求答题:
 ,则
,则 ;①
;①
 ,则
,则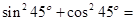 ;②
;②
 ,则
,则 .③
.③
……
观察上述等式,猜想:对任意锐角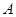 ,都有
,都有 .④
.④
(1)(3分)如图,在锐角三角形 中,利用三角函数的定义及勾股定理对
中,利用三角函数的定义及勾股定理对 证明你的猜想
证明你的猜想

(3分)已知: 为锐角
为锐角 且
且 ,求
,求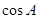 .
.
阅读下面的材料,先完成阅读填空,再将要求答题:
 ,则
,则 ; ①
; ①
 ,则
,则 ;
②
;
②
 ,则
,则 .
③
.
③
……
观察上述等式,猜想:对任意锐角A,都有 .④
.④
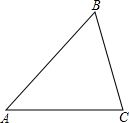
(1)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理对 证明你的猜想;
证明你的猜想;

(2)已知: 为锐角
为锐角 且
且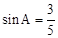 ,求
,求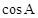 .
.
 阅读下面的材料,先完成阅读填空,再按要求答题:
阅读下面的材料,先完成阅读填空,再按要求答题: ,cos30°=
,cos30°= ,则sin230°+cos230°=______;①
,则sin230°+cos230°=______;① ,cos45°=
,cos45°= ,则sin245°+cos245°=______;②
,则sin245°+cos245°=______;② ,cos60°=
,cos60°= ,则sin260°+cos260°=______.③
,则sin260°+cos260°=______.③ ,求cosA.
,求cosA.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com