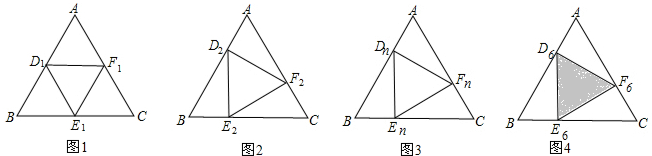
(2013•新华区一模)已知:等边△ABC的面积为S,D
n,E
n,F
n(n为正整数0分别是AB,BC,CA边上的点,连接D
nE
n,E
nF
n,F
nD
n,可得△D
nE
nF
n.
如图1,当AD
1=BE
1=CF
1=
AB时,我们容易得到△D
1E
1F
1是等边三角形,且
S△AD1F1=
S△D1E1F1=
S.
探究论证:
(1)如图2,当AD
2=BE
2=CF
2=
AB时,
①△D
2E
2F
2是
等边
等边
三角形(填写“等腰”或“等边”或“不等边”);
②
S△AD2F2=
;
S△D2E2F2=
(用含S的代数式表示);
③请说明以上结论的正确性.
猜想发现:
(2)如图3,当AD
n=BE
n=CF
n=
AB时,
①△D
nE
nF
n是
等边
等边
三角形(填写“等腰”或“等边”或“不等边”);
②
S△ADnFn=
;
S△DnEnFn=
(用含S的代数式表示).
实际应用:
(3)学校有一块面积为49m
2的等边△ABC空地,按如图4所示分割,其中AD
6=BE
6=CF
6=
AB,计划在△D
6E
6F
6内栽种花卉,其余地方铺草坪,则栽种花卉(即阴影部分)的面积为多少m
2?