
题目列表(包括答案和解析)
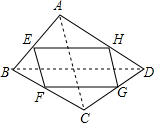
 如图,四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
如图,四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.| 1 | 4 |
 论,并加以证明;
论,并加以证明;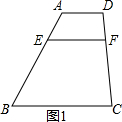 如图1,梯形ABCD中,AD∥BC,BC=a,AD=b,点E、F分别是两腰AB、CD上的点,且EF∥AD,设AE=d1、BE=d2,
如图1,梯形ABCD中,AD∥BC,BC=a,AD=b,点E、F分别是两腰AB、CD上的点,且EF∥AD,设AE=d1、BE=d2,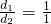 时,有EF=
时,有EF= ;
;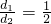 时,有EF=
时,有EF=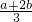 ;
;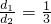 时,有EF=
时,有EF= ;
;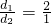 时,有EF=
时,有EF=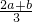 ;当
;当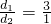 时,有EF=
时,有EF=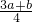 ;
;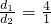 时,有
时,有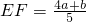 .
.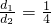 时,有EF=______;当
时,有EF=______;当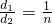 时,EF=______.
时,EF=______.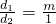 时,分别能得到什么结论(其中m、n均为正整数)并证明你的结论;
时,分别能得到什么结论(其中m、n均为正整数)并证明你的结论;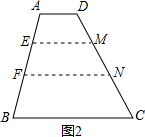
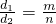 时,有何结论(其中m、n均为正整数)写出你的结论.
时,有何结论(其中m、n均为正整数)写出你的结论.如图,四边形ABCD中,E、F、G、日分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
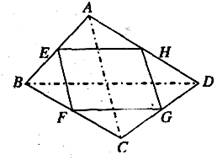
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形;
当四边形ABCD的对角线满足_____________时,四边形EFGH为矩形;
当四边形ABCD的对角线满足_____________时,四边形EFGH为正方形.
(2)探索△AEH、△CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明.
(3)如果四边形ABCD的面积为2.那么中点四边形EFGH的面积是多少?
 论,并加以证明;
论,并加以证明;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com