
题目列表(包括答案和解析)

 作图题
作图题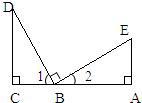 17、说理题:
17、说理题: (2007•安溪县质检)附加题:
(2007•安溪县质检)附加题: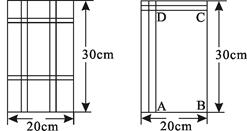
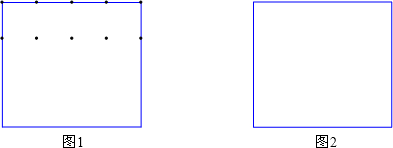
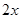 ,则每个竖彩条的宽为
,则每个竖彩条的宽为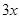 .为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形
.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形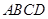 .
.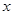 的代数式表示:
的代数式表示: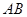 =____________________________cm;
=____________________________cm;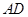 =____________________________cm;
=____________________________cm;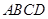 的面积为_____________cm
的面积为_____________cm ;
;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com