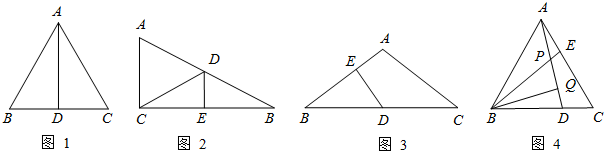
如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,
BD=CD=AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
请根据从上面材料中所得到的信息解答下列问题:
(1)△ABC中,若∠A:∠B:∠C=1:2:3,AB=a,则BC=______;
(2)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长=______.
(3)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA=______.
(4)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且∠CAD=∠ABE,AD、BE交于点P,作BQ⊥AD于Q,猜想PB与PQ的数量关系,并说明理由.


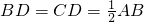 .于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.