2012年广东陆丰渔政大队指挥中心(A)接到海上呼救:一艘韩国货轮在陆丰碣石湾发生船体漏水,进水速度非常迅猛,情况十分危急,18名船员需要援救.经测量货轮B到海岸最近的点C的距离BC=20km,∠BAC=22°37′,指挥中心立即制定三种救援方案
(如图1):
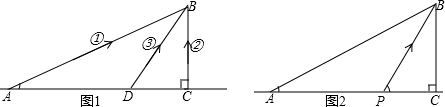
①派一艘冲锋舟直接从A开往B;②先用汽车将冲锋舟沿海岸线送到点C,然后再派冲锋舟前往B;③先用汽车将冲锋舟沿海岸线送到距指挥中心33km的点D,然后再派冲锋舟前往B.
已知冲锋舟在海上航行的速度为60km/h,汽车在海岸线上行驶的速度为90km/h.
(sin22°37′=
,cos22°37′=
,tan22°37′=
)
(1)通过计算比较,这三种方案中,哪种方案较好(汽车装卸冲锋舟的时间忽略不计)?
(2)事后,细心的小明发现,上面的三种方案都不是最佳方案,最佳方案应是:先用汽车将冲锋舟沿海岸线送到点P处,点P满足cos∠BPC=
(冲锋舟与汽车速度的比),然后再派冲锋舟前往B(如图2).
①利用现有数据,根据cos∠BPC=
,计算出汽车行AP加上冲锋舟行BP的总时间.
②在线段AC上任取一点M;然后用转化的思想,从几何的角度说明汽车行AM加上冲锋舟行BM的时间比车行AP加上冲锋舟行BP的时间要长.



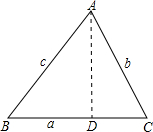 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.