
题目列表(包括答案和解析)
如图
1,在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°.若BC=1,则根据“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”以及勾股定理容易得到AB=________,AC=________.因此,含30°角的直角三角形三边(从小到大)之比为________;同样,如图2,含45°角的直角三角形三边(从小到大)之比为________.这样结合三角函数的定义可以推导得到30°、45°、60°角的三角函数值.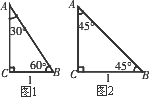
如图
1,在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°.若BC=1,则根据在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半及勾股定理容易得到AB=________,AC=________.因此,含30°角的直角三角形三边(从小到大)之比为________;同样,如图2,含45°角的直角三角形三边(从小到大)之比为________.这样结合三角函数的定义可以推导得到30°、45°、60°角的三角函数值.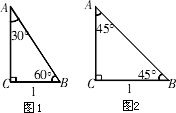
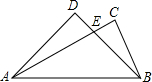 (创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,
(创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,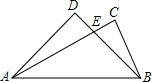 (创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,
(创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com