
题目列表(包括答案和解析)
| 1 | 2 |
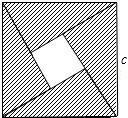
 95、小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
95、小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
小明、小敏两人一起做数学作业,小敏把题读到如图8(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说: “这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
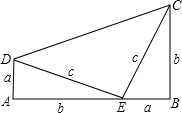
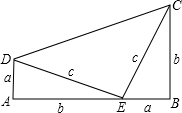
小明说:“小敏你错了,你未弄清本题的条件和结论,即使有CD⊥AB,BE⊥AC,公共角∠DAC=∠BAE,你的推理也是错误的.看我画的图8(2),显然△DAC与△EAB是不全等的.再说本题不是要证明∠B=∠C,而是要证明BE=CD.”
【小题1】根据小敏所读的题,判断“∠B=∠C”对吗?她的推理对吗?若不对,请做出正确的推理.
【小题2】根据小明说的,要证明BE=CD,必然是小敏丢了题中条件,请你把小敏丢的条件找回来,并根据找出的条件,你做出判断BE=CD的正确推理.
【小题3】要判断三角形全等,从这个问题中你得到了什么启发?
 ab
ab
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com