练习册

  • 练习册
  • 试题
    全等三角形的证明. 新授: 引入:两边及其中一边的对角对应相等的两个三角形全等吗?如果其中一边所对的角是直角呢? 定理:斜边和一条直角边对应相等的两个直角三角形全等. 这一定理可以简单地用“斜边.直角边 或“HL 表示. 已知:如图.△ABC和△A’B’C’中∠C=∠C’=90°.且AB=A’B’.BC=B’C’. 求证:△ABC≌△A’B’C’ 证明:Rt△ABC和Rt△A’B’C’中. ∵AB=A’B’.BC=B’C’.AC2=BC2-AB2 , A’C’2=B’C’2-A’B’2 ∵AC2=A’C’2 ∴AC=A’C’ ∴△ABC ≌A’B’C’(SSS) 做一做: 用三角尺可以作角平线.如图.在已知∠AOB的两边上分别取点M.N.使OM=ON.再过点M作OA的垂线.过点N作OB的垂线.两垂线交于点P.那么射线OP就是∠AOB的平分线 请证明: 证明: ∵MC=NC PC=PC ∴Rt△MCP≌Rt△NCP (HL) ∴∠MCP=∠NCP 议一议:如图.已知∠ACB=BDA=90°.要使△ACB≌△BDA.还需要什么条件?把它们分别写出来. 随堂练习 判断下列命题的真假.并说明理由. (1)两个锐角对应相等的两个直角三角形全等. (2)斜边及一锐角对应相等的两个直角三角形全等. (3)两条直角边对应相等的两个直角三角形全等. (4)一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等. 作业:P23 1.2 【查看更多】

     

    题目列表(包括答案和解析)

    10、下列所叙述的图形中，是全等三角形的只有（　　）

    查看答案和解析>>

    下列所叙述的图形中，是全等三角形的只有（　　）
    A．两边相等的两个直角三角形
    B．一边和一角对应相等的两个直角三角形
    C．边长为1厘米的两个等边三角形
    D．一个钝角相等的两个等腰三角形

    查看答案和解析>>

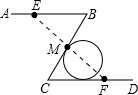    如图，在新修的小区中，有一条“Z”字形绿色长廊ABCD，其中AB∥CD，在AB，BC，CD三段绿色长廊上各修一小亭E，M，F，且BE=CF，点M是BC的中点，在凉亭M与F之间有一池塘，不能直接到达，要想知道M与F的距离，只需要测出线段
    EM
    EM
    的长度．理由是依据
    全等三角形的对应边相等
    全等三角形的对应边相等
    可以证明
    △BEM≌△CFM
    △BEM≌△CFM
    ，从而由全等三角形对应边相等得出．

    查看答案和解析>>

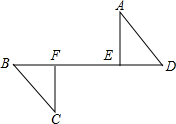    先填写完成第（1）小题中的空缺部分（数学表达式或理由），再按要求解答第（2）小题．
    如图：AD=CB，AE⊥BD，CF⊥BD，垂足分别是E、F，DF=BE．
    （1）求证：∠D=∠B；
    （2）请你连结AB、CD，探究AB与CD有何位置关系？并证明你的结论．
    证明：（1）∵AE⊥BD，CF⊥BD，
    ∴∠AED=∠
    CFB
    CFB
    =90°，
    ∵DF=BE，
    ∴DF-
    EF
    EF
    =BE-
    EF
    EF
    ，
    即DE=BF．
    在Rt△ADE和Rt△CBF中，
    方程组：
    ∴Rt△ADE≌Rt△CBF
    HL
    HL
    ，
    ∴∠D=∠B
    全等三角形的对应角相等
    全等三角形的对应角相等
    ．
    （2）

    查看答案和解析>>

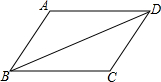    如图：AB∥CD，AD∥BC，求证：AB=CD．
    证明：∵AB∥CD
    ∴∠ABD=∠CDB
    （两直线平行，内错角相等）
    （两直线平行，内错角相等）
    ．
    ∵AD∥BC
    ∴∠ADB=∠CBD
    （两直线平行，内错角相等）
    （两直线平行，内错角相等）
    ．
    在△ABD和△CDB中
    ∠ADB=∠CBD
    ∵B=DB
    ∠ABD=∠CD
    ∴△ABD≌△CDB
    （ASA）
    （ASA）
    ．
    ∴AB=CD
    （全等三角形的对应边相等）
    （全等三角形的对应边相等）
    ．

    查看答案和解析>>


    同步练习册答案