
题目列表(包括答案和解析)
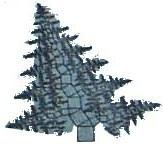 勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树,树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1,第二个正方形和第二个直角三角形的面积之和为S2,…,第n个正方形和第n个直角三角形的面积之和为Sn.设第一个正方形的边长为1.
勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树,树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1,第二个正方形和第二个直角三角形的面积之和为S2,…,第n个正方形和第n个直角三角形的面积之和为Sn.设第一个正方形的边长为1.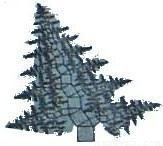

(2010四川乐山)勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.图(6)是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树,树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1,第二个正方形和第二个直角三角形的面积之和为S2,…,第n个正方形和第n个直角三角形的面积之和为Sn.设第一个正方形的边长为1.

图(6)
请解答下列问题:
(1)S1=__________;
(2)通过探究,用含n的代数式表示Sn,则Sn=__________.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com