练习册

  • 练习册
  • 试题
    问题一:“角平分线上的点到这个角的两边的距离相等 的逆命题是什么?试着说说看. 在一个角的内部.且到角的两边距离相等的点.在这个角的平分线上(让学生体会构造一个命题的逆命题.也是获得数学结论的一个途径) 问题二:你认为这个逆命题是真命题吗?如果是真命题.如何证明? 引导学生画图.写已知.求证.让学生自己完成证明 已知:如图.点P是∠AOB内部的一点.PD⊥OA于D.PE⊥OB于E.且PD=PE.求证:点P在∠AOB的平分线上 提示:连结OP证明OP是∠AOB的平分线上 问题三:在角的外部.有没有到角的两边距离相等的点?(角平分线的反向延长线上的点或这个角的邻补角的角平分线上的点都是到角的两边的距离相等的点) 问题四:“如果一个点到角的两边的距离不相等.那么这个点不在这个角的平分线上 你认为这个结论正确吗?如果正确.你怎样说明它的正确性?(让学生体会反证法的思想) 【查看更多】

     

    题目列表(包括答案和解析)

    平行四边形中有这样一类问题：已知一个平行四边形，求证另一个平行四边形．这类问题大都符合下面两个基本图形模式．

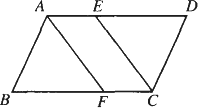
    基本图形一：如图，ABCD中，E，F分别是AD，BC边上的点，且AE＝CF．求证：四边形AFCE是平行四边形．

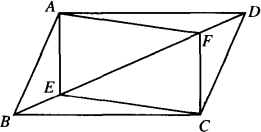
    基本图形二：如图，ABCD中，E，F是对角线BD上的两点，且BE＝DF．求证：四边形AECF是平行四边形．

    你能快速想到它们的证明方法吗？证明方法唯一吗？希望同学们注意基本图形的积累．

    查看答案和解析>>

    阅读材料：

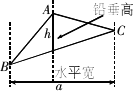
    如图，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”．我们可得出一种计算三角形面积的新方法：S△ABC＝ah，即三角形面积等于水平宽与铅垂高乘积的一半．

    解答下列问题：

    如图，抛物线顶点坐标为点C(1，4)，交x轴于点A(3，0)，交y轴于点B．

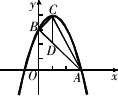
    (1)求抛物线和直线AB的解析式；

    (2)点P是抛物线(在第一象限内)上的一个动点，连接PA、PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB；

    (3)是否存在一点P，使S△PAB＝S△CAB，若存在，求出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    阅读下面材料：
    小伟遇到这样一个问题：如图1，在正方形ABCD中，点E、F分别为DC、BC边上的点，∠EAF=45°，连接EF，求证：DE+BF=EF．

    小伟是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段集中到同一条线段上．他先后尝试了平移、翻折、旋转的方法，发现通过旋转可以解决此问题．他的方法是将△ADE绕点A顺时针旋转90°得到△ABG（如图2），此时GF即是DE+BF．
    请回答：在图2中，∠GAF的度数是______．
    参考小伟得到的结论和思考问题的方法，解决下列问题：
    （1）如图3，在直角梯形ABCD中，AD∥BC（AD＞BC），∠D=90°，AD=CD=10，E是CD上一点，若∠BAE=45°，DE=4，则BE=______．
    （2）如图4，在平面直角坐标系xOy中，点B是x轴上一动点，且点A（-3，2），连接AB和AO，并以AB为边向上作正方形ABCD，若C（x，y），试用含x的代数式表示y，则y=______．

    查看答案和解析>>

    探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：
    （1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；
    （2）请你直接利用以上结论，解决以下三个问题：
    ①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A=50°，则∠ABX+∠ACX= _________ °；
    ②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=50°，∠DBE=130°，求∠DCE的度数；
    ③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC=140°，∠BG1C=77°，求∠A的度数．

    查看答案和解析>>

    阅读下面材料：

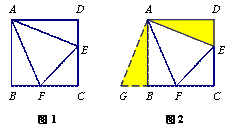
    小伟遇到这样一个问题：如图1，在正方形ABCD中，点E、F分别为DC、BC边上的点，∠EAF=45°，连结EF，求证：DE+BF=EF．

     


    小伟是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段集中到同一条线段上．他先后尝试了平移、翻折、旋转的方法，发现通过旋转可以解决此问题．他的方法是将△ADE绕点A顺时针旋转90°得到△ABG（如图2），此时GF即是DE+BF．

    请回答：在图2中，∠GAF的度数是        ．

    参考小伟得到的结论和思考问题的方法，解决下列问题：

    （1）如图3，在直角梯形ABCD中，AD∥BC（AD＞BC），∠D=90°，AD=CD=10，E是CD上一点，若∠BAE=45°，DE=4，则BE=         ．

    （2）如图4，在平面直角坐标系xOy中，点B是x轴上一动点，且点A（，2），连结AB和AO，并以AB为边向上作正方形ABCD，若C（x，y），试用含x的代数式表示y，则y=              ．

    查看答案和解析>>


    同步练习册答案