
题目列表(包括答案和解析)
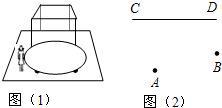 19、如图(1),在足球比赛中,球员射中球门的难易程度与他所处的位置的射门角度的大小有关.如果在一次比赛中,小华和小勇分别处在图(2)中的A,B两点,球门的位置在线段CD,如果球在小华的脚下,此时他应该选择传给小勇还是自己射门较好?(通过尺规作图说明原因)
19、如图(1),在足球比赛中,球员射中球门的难易程度与他所处的位置的射门角度的大小有关.如果在一次比赛中,小华和小勇分别处在图(2)中的A,B两点,球门的位置在线段CD,如果球在小华的脚下,此时他应该选择传给小勇还是自己射门较好?(通过尺规作图说明原因)| 32 | 3 |
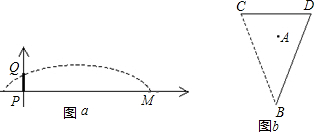
 米.如图a:以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问:
米.如图a:以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问: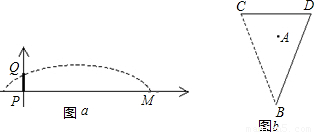
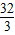 米.如图a:以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问:
米.如图a:以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问:
 米.如图a:以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问:
米.如图a:以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问: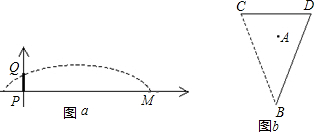
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com