为加速森林重庆建设,重庆市委书记薄熙来号召:“动员三千万民众,绿化八百万山川”.是政府决定对树苗育苗基地实行政府补贴,规定每年培育一亩树苗一次性补贴若干元,随着补贴数字的不断增大,某地苗圃每年育苗规模也不断增加,但每年每亩苗圃的收益会相应下降,经调查每年培植亩数y(亩)与政府每亩补贴数额x(元)之间有如下关系(政府补贴为100元的整数倍,且每亩补贴不超过1000元):
| x(元) |
0 |
100 |
200 |
300 |
400 |
| y(亩) |
600 |
1000 |
1400 |
1800 |
2200 |
而每年每亩的收益p(元)与政府每亩补贴数额x(元)之间满足一次函数p=-5x+9000.
(1)请观察题中的表格,用学过的一次函数、反比例函数或二次函数的有关知识求出育苗亩数y(亩)与政府每亩补贴数额x(元)之间的函数关系式;
(2)当2010年政府补贴每亩数额x(元)是多少元时,该地区苗圃的收益w(元)最大,最大收益是多少?
(3)在2010年苗圃取得最大收益的育苗情况下,该地区培植面积刚好达到最大化,要想增收,只能提高每亩收益.经市场调查,培育银杏树苗畅销,每亩的经济效益相应会更好.2011年该地区用去年培育面积的(30-a)%的土地培育银杏树苗,其余面积继续培育一般类树苗,预计今年培育银杏树苗每亩收益在去年培育一般类树苗每亩收益的基础上增加了(100+3a)%,由于培育银杏树苗每亩多支出1000元,2011年该地区因培育银杏类树苗预计比去年增收399万元.请参考以下数据,通过计算,估算出a的整数值.(参考数据:
=5.916,
=6.082,
=6.244)

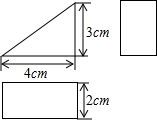 已知一个几何体的三视图的有关尺寸如图所示,请写出这个几何体的名称,并计算这个几何体的表面积(表面积=底面积+侧面积).
已知一个几何体的三视图的有关尺寸如图所示,请写出这个几何体的名称,并计算这个几何体的表面积(表面积=底面积+侧面积).