
题目列表(包括答案和解析)
 问题解决.
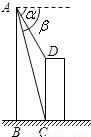
问题解决.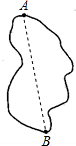 如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B之间的距离,但绳子不够长,你能帮他想个主意测量吗?并说明你的理由.用这种方法能解决你身边的实际问题吗?试举一例说明.
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B之间的距离,但绳子不够长,你能帮他想个主意测量吗?并说明你的理由.用这种方法能解决你身边的实际问题吗?试举一例说明.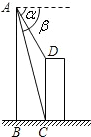 关于三角函数有如下的公式:
关于三角函数有如下的公式:| tanα+tanβ |
| 1-tanα•tanβ |
| tan45°+tan60° |
| 1-tan45°•tan60° |
1+
| ||
1-1•
|
(1+
| ||||
(1-
|
| 3 |
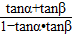 ③
③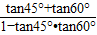 =
=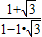 =
=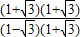 =-(2+
=-(2+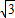 ).
).
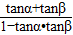 ③
③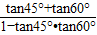 =
=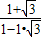 =
= =-(2+
=-(2+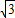 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com