
题目列表(包括答案和解析)
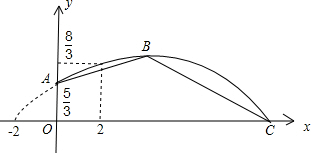 铅球从A点被推出,实线部分表示铅球所经过的路线)
铅球从A点被推出,实线部分表示铅球所经过的路线)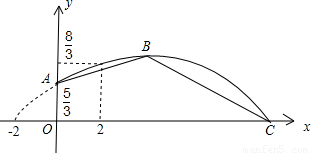
如果两个正数 ,即
,即![]() ,有下面的不等式:
,有下面的不等式:
![]() 当且仅当
当且仅当![]() 时取到等号
时取到等号
我们把 叫做正数
叫做正数![]() 的算术平均数,把
的算术平均数,把![]() 叫做正数
叫做正数![]() 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知 ,求函数
,求函数![]() 的最小值。
的最小值。
解:令 ,则有
,则有![]() ,得
,得![]() ,当且仅当
,当且仅当![]() 时,即
时,即![]() 时,函数有最小值,最小值为
时,函数有最小值,最小值为![]() 。
。
根据上面回答下列问题
1.已知 ,则当
,则当![]() 时,函数
时,函数![]() 取到最小值,最小值
取到最小值,最小值
为
2.用篱笆围一个面积为![]() 的矩形花园,问这个矩形的长、宽各为多少时,所
的矩形花园,问这个矩形的长、宽各为多少时,所
用的篱笆最短,最短的篱笆周长是多少
3.已知![]() ,则自变量
,则自变量![]() 取何值时,函数
取何值时,函数![]() 取到最大值,最大值为多少?
取到最大值,最大值为多少?

如果两个正数 ,即
,即 ,有下面的不等式:
,有下面的不等式:
 当且仅当
当且仅当 时取到等号
时取到等号
我们把 叫做正数
叫做正数 的算术平均数,把
的算术平均数,把 叫做正数
叫做正数 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知 ,求函数
,求函数 的最小值。
的最小值。
解:令 ,则有
,则有 ,得
,得 ,当且仅当
,当且仅当 时,即
时,即 时,函数有最小值,最小值为
时,函数有最小值,最小值为 。
。
根据上面回答下列问题
1.已知 ,则当
,则当 时,函数
时,函数 取到最小值,最小值
取到最小值,最小值
为
2.用篱笆围一个面积为 的矩形花园,问这个矩形的长、宽各为多少时,所
的矩形花园,问这个矩形的长、宽各为多少时,所
用的篱笆最短,最短的篱笆周长是多少
3.已知 ,则自变量
,则自变量 取何值时,函数
取何值时,函数 取到最大值,最大值为多少?
取到最大值,最大值为多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com