如图，梯形ABCD中，AD∥BC，BA＝AD＝DC，点E在CB延长线上，BE＝AD，连接AC、AE．（1）求证：AE＝AC（2）若AB⊥AC， F是BC的中点，试判断四边形AFCD的形状，并说明理由．

【解析】根据平行四边形的性质和菱形的性质求证

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.

（1）求证：∠DAF＝∠CDE

（2）问△ADF与△DEC相似吗？为什么？

（3）若AB＝4,AD＝3,AE＝3,求AF的长.

【解析】此题考核平行四边形的性质，相似三角形的判定和性质

    数学习题课上，数学老师布置了这样一道练习：

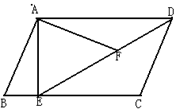
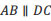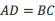四边形中，有下列三个论断:① ;②;③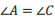;请以其中两个论断作为题设，另一个论断作为结论，写出一个你认为正确的命题.李梅同学写出了命题1：已知四边形中，，，则.王华同学写出了命题2：已知四边形中，，，则.你认为命题1和命题2都正确吗？若正确，请加以证明；若不正确，请举反例说明理由.

【解析】根据平行四边形的性质求证

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.

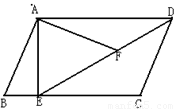
（1）求证：∠DAF＝∠CDE[来源:Zxxk.Com]

（2）问△ADF与△DEC相似吗？为什么？

（3）若AB＝4,AD＝3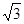,AE＝3,求AF的长.

【解析】此题考核平行四边形的性质，相似三角形的判定和性质

    数学习题课上，数学老师布置了这样一道练习：

四边形中，有下列三个论断:① ;②;③;请以其中两个论断作为题设，另一个论断作为结论，写出一个你认为正确的命题.李梅同学写出了命题1：已知四边形中，，，则.王华同学写出了命题2：已知四边形中，，，则.你认为命题1和命题2都正确吗？若正确，请加以证明；若不正确，请举反例说明理由.

【解析】根据平行四边形的性质求证