同学们，闹钟都见过吧！它的时针和分针如同兄弟俩在赛跑，可你是否知道时针每分钟走多少度？分针每分针走多少度？当你弄清楚这个问题后，你能解决很多关于闹钟有趣的问题：
（1）三点整时时针与分针所夹的角是______度．
（2）7点25分时针与分针所夹的角是______度．
（3）一昼夜（0点到24点）时针与分针互相垂直的次数有多少次？

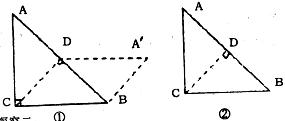
把一个等腰Rt△ABC；沿斜边上的离线CD(裁剪线)剪一刀，从这一个三角形中裁下一部分，与剩下部分能拼成一个平行四边形见示意图①．以下探究过程中有画图要求的，工具不限，不必写画法和证明．

探究一：

(1)想一想――判断四边形是平行四边形的依据．

(2)做一做――按上述的裁剪方法，请你拼一个与图①位置或形状不同的平行四边形，并在图②中画出示意图．

探究二：

在等腰Rt△ABC中．请你找出其它的裁剪线，把分割成的两部分拼出不同类型的特殊四边形．

(1)试一试――你能拼得所有不同类型的特殊四边形有_________；

他们的裁剪线分别是_______；

(2)画一画――请在图③中画出一个你拼得的特殊四边形示意图．