
题目列表(包括答案和解析)
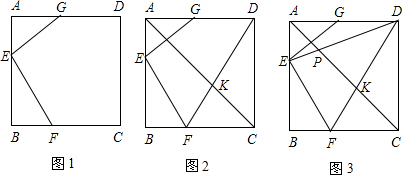
| 2 |
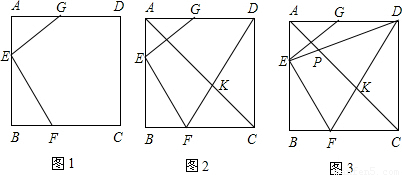
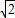 .△BEF的周长为24,求PK的长.
.△BEF的周长为24,求PK的长. 25、如图①,在正方形ABCD中,P是对角线AC上一点,PE⊥AB,PF⊥BC垂足分别为,E、F,
25、如图①,在正方形ABCD中,P是对角线AC上一点,PE⊥AB,PF⊥BC垂足分别为,E、F,
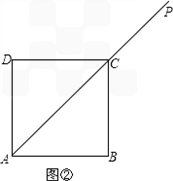
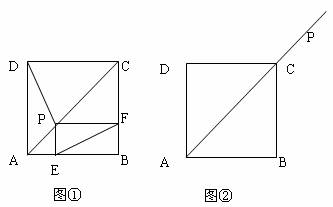
如图①,在正方形ABCD中,P是对角线AC上一点,PE⊥AB,PF⊥BC垂足分别为,E、F,(1)请你猜想EF和PD有何关系,并证明。
(2)如图②若点P是对角线AC延长线上任意一点,其它条件不变,请根据已知补全图形,并判断(1)中你所猜想的结论还成立吗?(不需要证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com