
题目列表(包括答案和解析)
阅读材料:黑白双雄、纵横江湖;双剑合璧,天下无敌。这是武侠小说中常见的描述,其意是指两人合在一起,取长补短,威力无比。在二次根式中也有这种相辅相成的“对子”如: ,
, 与
与 的积不含有根号,我们就说这两个式子互为有理化因式,其中一个是另一个的有理化因式。于是二次根式
的积不含有根号,我们就说这两个式子互为有理化因式,其中一个是另一个的有理化因式。于是二次根式 可以这样解:
可以这样解: ,像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化。
,像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化。
解决问题:①  的有理化因式是_______________
的有理化因式是_______________
②计算:
③计算:
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1) 的有理化因式是 .
的有理化因式是 .  分母有理化得 .
分母有理化得 .
(2)分母有理化:(1)  ="_________;(2)"
="_________;(2)"  ="________;(3)"
="________;(3)"  =______..
=______..
(3)计算:  .
.
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1) 的有理化因式是
.
的有理化因式是
.  分母有理化得
.
分母有理化得
.
(2)分母有理化:(1)  =_________;(2)
=_________;(2)
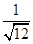 =________;(3)
=________;(3)
 =______..
=______..
(3)计算:  .
.
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1)  的有理化因式是 .
的有理化因式是 . 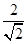 分母有理化得 .
分母有理化得 .
(2)分母有理化:(1)  ="_________;(2)"
="_________;(2)"  ="________;(3)"
="________;(3)" 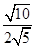 =______..
=______..
(3)计算:  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com