
题目列表(包括答案和解析)


操作实验: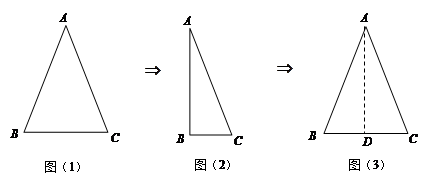
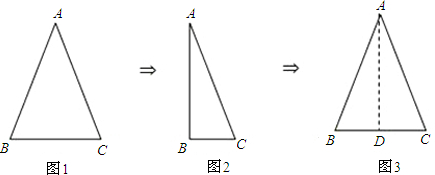
如图,把等腰三角形沿顶角平分线对折并展开,发现被折痕分成的两个三角形成轴对称.
所以△ABD≌△ACD,所以∠B=∠C.
归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等.
根据上述内容,回答下列问题:
思考验证:
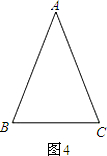
如图(4),在△ABC中,AB=AC.
试说明∠B=∠C的理由.(添加辅助线说明)
探究应用:
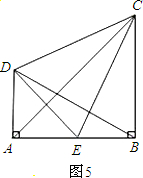
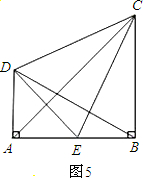
如图(5),CB⊥AB,垂足为B,DA⊥AB,垂足为A.E为AB的中点,AB=BC,CE⊥BD于F,连接DC、DE、AC,AC与 DE交于点O.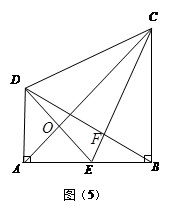
(1)BE与AD是否相等?为什么?
(2)小明认为AC垂直平分线段DE,你认为对吗?说说你的理由。
(3)∠DBC与∠DCB相等吗?试说明理由.
操作实验:
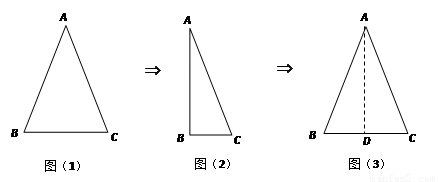
如图,把等腰三角形沿顶角平分线对折并展开,发现被折痕分成的两个三角形成轴对称.
所以△ABD≌△ACD,所以∠B=∠C.
归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等.
根据上述内容,回答下列问题:
思考验证:
如图(4),在△ABC中,AB=AC.

试说明∠B=∠C的理由.(添加辅助线说明)
探究应用:
如图(5),CB⊥AB,垂足为B,DA⊥AB,垂足为A.E为AB的中点,AB=BC,CE⊥BD于F,连接DC、DE、AC,AC与 DE交于点O.
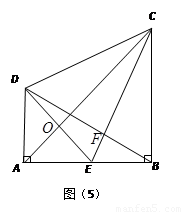
(1)BE与AD是否相等?为什么?
(2)小明认为AC垂直平分线段DE,你认为对吗?说说你的理由。
(3)∠DBC与∠DCB相等吗?试说明理由.



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com