
题目列表(包括答案和解析)
 我们给出如下定义:三角形三条中线的交点称为三角形的重心.一个三角形有且只有一个重心.可以证明三角形的重心与顶点的距离等于它与对边中点的距离的两倍.
我们给出如下定义:三角形三条中线的交点称为三角形的重心.一个三角形有且只有一个重心.可以证明三角形的重心与顶点的距离等于它与对边中点的距离的两倍.
我们给出如下定义:三角形三条中线的交点称为三角形的重心.一个三角形有且只有一个重心.可以证明三角形的重心与顶点的距离等于它与对边中点的距离的两倍.
可以根据上述三角形重心的定义及性质知识解答下列问题:
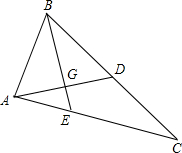
如图,∠B的平分线BE与BC边上的中线AD互相垂直,并且BE=AD=4

(1)猜想AG与GD的数量关系,并说明理由;
(2)求△ABC的三边长.
如图,已知:⊙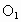 与⊙
与⊙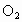 相交于A,B两点,经过A点的直线分别交⊙
相交于A,B两点,经过A点的直线分别交⊙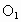 ,⊙
,⊙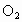 于C,D两点(C,D不与B重合),连结BD,过D作BD的平行线交⊙
于C,D两点(C,D不与B重合),连结BD,过D作BD的平行线交⊙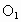 于点E,连结BE.
于点E,连结BE.
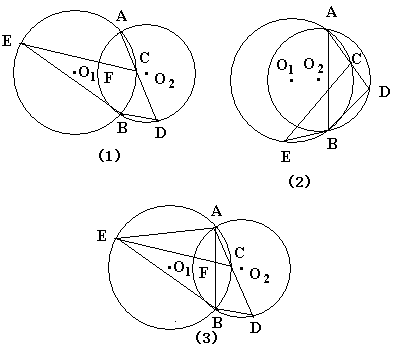
(1)求证:BE是⊙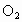 的切线.(图(1))
的切线.(图(1))
(2)如图(2),若两圆圆心在公共弦AB的同侧,其他条件不变,判断BE和⊙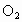 的位置关系.(不要求证明)
的位置关系.(不要求证明)
(3)若点C为劣弧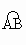 的中点,其他条件不变,连结AB,AE,AB与CE交于点F,如图(3),写出图中所有的相似三角形.(不另外连线,不要求证明)
的中点,其他条件不变,连结AB,AE,AB与CE交于点F,如图(3),写出图中所有的相似三角形.(不另外连线,不要求证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com