
可建立空间直角坐标系A-xyz,由平面几何知
识知:AD=4,D(O,4,O),B(2,0,0)。
C(2,2,0),P(0,0,2),E(0,0,1),
F(1,0,1),G(1,1,1).……………2分
(1) =(1,0,1),
=(1,0,1), =(一1,1,1),
=(一1,1,1),
∴ ?
? =0
=0
∴AF与BG所成的角为 ……………………………4分
……………………………4分
(2)可证明AD⊥平面APB,平面APB的法向量为n(0,1,0)
设平面CPD的法向量为m=(1, y, z),由
∴ m=(1,1,2) ……………………………………………………10分
∴  …………………………12分
…………………………12分
19.解:填湖面积 填湖及排水设备费 水面经济收益 填湖造地后收益
x(亩)
ax2(元)
bx
cx
(1)收益不小于指出的条件可以表示为 ,
,
所以 .……………………………………3分
.……………………………………3分
显然a>0,又c>b
∴ 时,此时所填面积的最大值为
时,此时所填面积的最大值为 亩……………………………7分
亩……………………………7分
(2)设该地现在水面m亩.今年填湖造地y亩,
则 ,………………9分
,………………9分
即 ,所以
,所以 .
.
因此今年填湖造地面积最多只能占现有水面的 ………………………………12分
………………………………12分
20.(本小题满分12分)
解:(1)根据导数的几何意义知f(x)=g′(x)=x2+ax-b
由已知-2、4是方程x2+ax-b=0的两个实根
由韦达定理, ,………………5分
,………………5分
(2)g(x)在区间[一1,3]上是单调递减函数,所以在[一1,3]区间上恒有
 横成立
横成立
这只需满足
而a2+b2可视为平面区域 内的点到原点距离的平方,其中点(-2,3)距离原点最近.所以当
内的点到原点距离的平方,其中点(-2,3)距离原点最近.所以当 时,a2+b2 有最小值13. ………………………………12分
时,a2+b2 有最小值13. ………………………………12分
21.解(1)A(a,0),B(0,b),P(x,y)
 ,即
,即 ……………………………2分
……………………………2分
 ,由题意知t>0,
,由题意知t>0,
 即
即
 点P的轨迹方程C为:
点P的轨迹方程C为: .…………………………4分
.…………………………4分
(2). T=2 时,C为 .………………………………………5分
.………………………………………5分
设M(x1,y1),则N(-x1,-y1),则MN=
设直线MN的方程为
点Q到MN距离为
 …………………………………………………………………………7分
…………………………………………………………………………7分
∴SΔQMN= .…………………………………8分
.…………………………………8分
∵S2ΔQMN=
又
∴S2ΔQMN=4?9x1y1
而
∴ …………………………………………………………11分
…………………………………………………………11分
即
当且仅当 时,等号成立
时,等号成立
∴SΔQMN的最大值为 ……………………………………………………12分
……………………………………………………12分
22.(1)证明: ,因为对称轴
,因为对称轴 ,所以在[0,1]上为增函数,
,所以在[0,1]上为增函数, .……………………………………………………4分
.……………………………………………………4分
(2)解:由
得
两式相减得 , ………………7分
, ………………7分
当n=1时,b1=S1=1
当nㄒ2时,
即 ………………9分
………………9分
(3)解:由(1)与(2)得 …………10分
…………10分
假设存在正整数k时,使得对于任意的正整数n,都有cnㄑck成立,
当n=1,2时,c2-c1= c2> c1
c2> c1
当n =2时,cn+1-cn=(
=2时,cn+1-cn=( )n-2
)n-2
 ,
,
所以当n<8时,cn+1>cn,
当n=8时,cn+1=cn
当n>8时,cn+1<cn, ……………………13分
所以存在正整数k=9,使得对于任意的正整数n,都有cn ck成立。 …………14分
ck成立。 …………14分



 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( )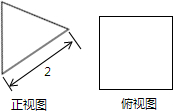 一个几何体的三视图如图所示,其中正视图是一个边长为2的正三角形,俯视图是一正方形,那么该几何体的侧视图的面积为( )
一个几何体的三视图如图所示,其中正视图是一个边长为2的正三角形,俯视图是一正方形,那么该几何体的侧视图的面积为( ) 一个几何体的三视图如图所示,其中正视图和左视图均为边长是
一个几何体的三视图如图所示,其中正视图和左视图均为边长是 14.20 15.32 16.
14.20 15.32 16.
 ………………2分
………………2分 .………………………………4分
.………………………………4分 .…………………6分
.…………………6分 ,
, ,………………………………………8分
,………………………………………8分 …………………………………………10分
…………………………………………10分 …………………………………………12分
…………………………………………12分