练习册

  • 练习册
  • 试题
    类比是发现新知.寻找规律.解决问题的一个重要的方法. 【查看更多】

     

    题目列表(包括答案和解析)

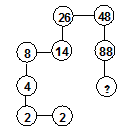
    猜想规律型问题是目前中考的一大热点，原因在于猜想本身就是重要的数学方法，更是人们探索发现知识的重要手段．此类题不但能培养学生分析、归纳、解决问题的能力，也非常有利于学生创造性思维的培养．对于有关图形的规律探索问题，更能考查学生的观察读图能力．笔者认为做此类题不妨在用眼观察的同时也用笔做一有序列举，

    查看答案和解析>>

    观察下列依次排列的一些数，你能发现它们具有什么规律？它后面的三个数可能是什么数？试将它们写出来。
    （1）4，-3，2，-l，0，1，-2，3，…；
    （2）-1，3，-9，27，-81，…。

    查看答案和解析>>

    观察下图并寻找规律，“？”处的数字是（    ）。

    查看答案和解析>>

    应用规律，解决问题
    （1）．定义：a为不等于1的有理数，我们把
    1
    1-a
    称为a的差倒数，如：2的差倒数是
    1
    1-2
    =
    1
    -1
    =-1    ，-1的差倒数是
    1
    1-(-1)
    =
    1
    2
    ，已知a1=-
    1
    3
    ，
    ①a2是a1的差倒数，则a2=
    3
    4
    3
    4
    ．
    ②a3是a2的差倒数，则a3=
    4
    4
    ．
    ③a4是a3的差倒数，则a4=
    -
    1
    3
    -
    1
    3
    ．
    ④以此类推，a2011=
    -
    1
    3
    -
    1
    3
    ．
    （2）．我们知道：
    1
    2
    ×
    2
    3
    =
    1
    3
    ，
    1
    2
    ×
    2
    3
    ×
    3
    4
    =
    1
    4
    ，…，
    1
    2
    ×
    2
    3
    ×
    3
    4
    ×    …×
    n
    n+1
    =
    1
    n+1
    ，试根据上面规律，
    计算：(
    1
    19
    -1)(
    1
    20
    -1)(
    1
    21
    -1)    …(
    1
    2011
    -1)    ．

    查看答案和解析>>

    观察下列方程和等式，寻找规律，完成问题：
    ①方程x2-7x+6=0，x1=1，x2=6，而x2-7x+6=（x-1）（x-6）；
    ②方程x2-4x-5=0，x1=5，x2=-1，而x2-4x-5=（x-5）（x+1）；
    ③方程4x2-12x+9=0，x1=
    3
    2
    ，x2=
    3
    2
    ，而4x2-12x+9=4(x-
    3
    2
    )(x-
    3
    2
    )    ；
    ④方程3x2+7x+4=0，x1=-
    4
    3
    ，x2=-1，而3x2+7x+4=3(x+
    4
    3
    )(x+1)    ；…
    （1）探究规律：当方程ax2+bx+c=0（a≠0）时，
     
    ；
    （2）解决问题：根据上述材料将下列多项式分解：x2-x-2；2x2+3x-2
    （3）拓广应用：已知，如图，现有1×1，a×a的正方形纸片和1×a的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为2a2+5a+2，并标出此矩形的长和宽．
    精英家教网

    查看答案和解析>>


    同步练习册答案