
题目列表(包括答案和解析)
|
|
|
|
|
|
|
|
|
|
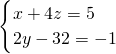 (2)
(2)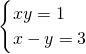 (3)
(3)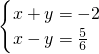 (4)
(4)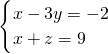 (5)
(5)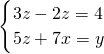 .
.下列说法中正确的是( )
A.二元一次方程中只有一个解
B.二元一次方程组有无数个解
C.二元一次方程组的解必是它所含的二元一次方程的公共解
D.判断一组解是否为二元一次方程组的解,只需代入其中的一个二元一次方程即可
下列说法中正确的是( )
A.二元一次方程中只有一个解 B.二元一次方程组有无数个解
C.二元一次方程组的解必是它所含的二元一次方程的公共解
D.判断一组解是否为二元一次方程的解,只需代入其中的一个二元一次方程即可
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com