
题目列表(包括答案和解析)
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 16 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 16 |
| 3 |
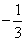 x3+
x3+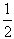 x2+2ax,
x2+2ax,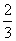 ,+∞)上存在单调递增区间,求a的取值范围;
,+∞)上存在单调递增区间,求a的取值范围;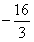 ,求f(x)在该区间上的最大值。
,求f(x)在该区间上的最大值。 | 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 16 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |
一、选择题:(本大题共12小题.每小题5分,共60分)
ABBBC BDDCB BA
二、填空题:(共4小题,每小题4分,共16分.)
13.17π 14.4 15. (1.0) 16.24
15. (1.0) 16.24
三、解答题:(共6小题,共74分)
17.解:(1)∵f(x)=2cos2x+ sin2x+m=2sin(2x+
sin2x+m=2sin(2x+ )+m+1,…………………2分
)+m+1,…………………2分
∴函数f(x)的最小正周期T=π.…………………………………………………4分
在[0, π]上单调递增区间为[0,  ],[+
],[+ ]………6分
]………6分
(2)当x∈[0,  ]时,∵f(x)递增,∴当x=
]时,∵f(x)递增,∴当x= 时,f(x)最大值为m+3=4,即m+3=4,
时,f(x)最大值为m+3=4,即m+3=4,
解得m=1∴m的值为1.………………………………………………………12分
18.(1)由题意,得 …………3分
…………3分

 0≤x≤50 …………6分
0≤x≤50 …………6分
(2)设该市第二、三产业的总产值增加f(x) (0<x≤5)万元,则
f(x)=(100-x)(1+2x%)a-100a+1.2ax
=- 。…………10分
。…………10分
∵x∈(0,50]时,f(x)单调递增,∴x=50时,f(x)max=60a,
即应分流出50万人才能使该市第二、三产业的总产值增加最多……………12分
 19.(本小题12分)
19.(本小题12分)
解:(1) ∵M为AB中点,D为PB中点,
∴MD∥AP,又∴MD 平面ABC
平面ABC
∴DM ∥平面APC……………………3分
(2)∵ΔPMB为正三角形,且D为PB中点
∴MD⊥PB
又由(1) ∴知MD⊥AP, ∴AP⊥PB
又已知AP⊥PC ∴AP⊥平面PBC
∴BC⊥平面APC
∴平面ABC⊥平面APC ………………8分
(3)∵AB=20
∴MB=10 ∴PB=10
又BC=4,PC=
∴SΔBDC= ΔPBC=
ΔPBC=
又MD= AP=
AP=
 =5
=5
∴VD-BCM=VM-BCD= SΔBDC
SΔBDC ----------------------12分
----------------------12分
20.(本小题满分12分) )
解:(1)根据导数的几何意义知f(x)=g′(x)=x2+ax-b
由已知一2、4是方程x2+ax-b =0的两个实根-
由韦达定理, ,∴
,∴ ,f(x)= x2-2x-8-----------------------5分
,f(x)= x2-2x-8-----------------------5分
(2)g(x)在区间【-1.3】上是单调递减函数,所以在【-1,3】区间上恒有
f(x)=g’(x)=x2+ax-b≤0,即f(x)=g’(x)=x2+ax-b≤0在【-1,3】恒成立,
这只需要满足 即可,也即
即可,也即
而a2+b2可以视为平面区域 内的点到原点距离的平方,其中点(-2,3)距离原点最近,所以当
内的点到原点距离的平方,其中点(-2,3)距离原点最近,所以当 时,a2+b2有最小值13---------------------------------------12分
时,a2+b2有最小值13---------------------------------------12分
21.(本题满分12分)
(1)bl=1,;b2=4;b3=10;b4=22;b5=46:
可见:b2-2 bl=2;b3-2 b2=2;b4-2 b3=2;b5-2 b4=2
猜测:bn+1-2 bn=2 (或bn+1=2 bn+2或bn+1- bn=3×2n-1)……………………………4分
(2)由(1)
 …………………………………………6分
…………………………………………6分
所以{bn+2},是以b1+2=3为首项,2为公比的等比数列,
∴ bn+2=3×2n-1 ,即bn =3×2n-1-2。。-
(注:若考虑, 且不讨论n=1,扣1分)……………………………………8分
且不讨论n=1,扣1分)……………………………………8分
(3)若数列{ bn }中存在不同的三项bp, bq , br(p,q,r∈N)恰好成等差数列,不妨设p>q>r,显然,{ bn }是递增数列,则2 bq= bp, + br------------------------------------------------------9分
即2×(3×2q-1-2)=(3×2p-1-2)+(3×2r-1-2),于是2×2q-r=2q-r+1------------10分
由p,q,r∈N且p>q>r知,q-r≥1,p-r≥2
∴等式的左边为偶数,右边为奇数,不成立,故数列{bn}中不存在不同的三项bp,bq,br(p,q,r∈N)恰好成等差数列------------------------------------------------------------------------12分
22.(本小题满分12分)
(1)解:设椭圆C的方程为 (a>b>0),-------------------------------- 1分
(a>b>0),-------------------------------- 1分
抛物线方程化为x2=4y,其焦点为(0,1)------------------------------------------------------2分
则椭圆C的一个顶点为(0,1),即b=1-----------------------------------3分
由 ,
,
所以椭圆C的标准方程为
(2)证明:易求出椭圆C的右焦点F(2,0),
设A(x1,y1),B(x2,y2),M(0,y0),显然直线l的斜率存在
设直线l的方程为y=k(x-2),代入方程 +y2=1并整理,
+y2=1并整理,
得(1+5k2)x2-20k2x+20k2-5=0--------------------------------------------------------------9分
∴x1+x2= , x1 x2=
, x1 x2= --------------------------------------------------------10分
--------------------------------------------------------10分
又,

即(x1-0,y1-y0)= (2- x1,- y1),( x2-0, y2-y0)=
(2- x1,- y1),( x2-0, y2-y0)=
 (2- x2,- y2)
(2- x2,- y2)
∴ ,-------------------------------------------------------------12分
,-------------------------------------------------------------12分
所以 ………………14分
………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com