
题目列表(包括答案和解析)
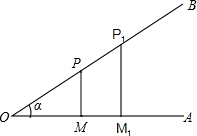 课本中,是这样引入“锐角三角函数”的:如图,在锐角α的终边OB上,任意取两点P和P1,分别过点P和P1做始边OA的垂线PM和P1M1,M和M1为垂足.我们规定,比值
课本中,是这样引入“锐角三角函数”的:如图,在锐角α的终边OB上,任意取两点P和P1,分别过点P和P1做始边OA的垂线PM和P1M1,M和M1为垂足.我们规定,比值如图,在正方形ABCD中,E为对角线AC上一点,联结EB、ED,延长BE交AD于点F.
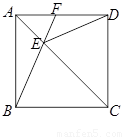
(1)求证:∠BEC =∠DEC ;
(2)当CE=CD时,求证: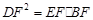 .
.
【解析】此题主要考核全等三角形的性质和相似三角形的性质
 课本中,是这样引入“锐角三角函数”的:如图,在锐角α的终边OB上,任意取两点P和P1,分别过点P和P1做始边OA的垂线PM和P1M1,M和M1为垂足.我们规定,比值________叫做角α的正弦,比值________叫做角α的余弦.这是因为,由相似三角形的性质,可推得关于这些比值得两个等式:________,________.说明这些比值都是由________唯一确定的,而与P点在角的终边上的位置无关,所以,这些比值都是自变量α的函数.
课本中,是这样引入“锐角三角函数”的:如图,在锐角α的终边OB上,任意取两点P和P1,分别过点P和P1做始边OA的垂线PM和P1M1,M和M1为垂足.我们规定,比值________叫做角α的正弦,比值________叫做角α的余弦.这是因为,由相似三角形的性质,可推得关于这些比值得两个等式:________,________.说明这些比值都是由________唯一确定的,而与P点在角的终边上的位置无关,所以,这些比值都是自变量α的函数.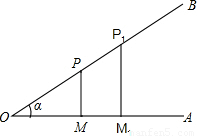
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com