
题目列表(包括答案和解析)
| 2010! |
| 2009! |
在数学中定义了一种运算符号“!”它表示的含义如下:如:
1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,
由此,请同学们思考 的值为
的值为
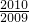

| A、一组数据-2,-1,0,1,2的方差是3 | ||
| B、要了解一批新型导弹的性能,采用抽样调查的方式 | ||
| C、购买一张福利彩票,中奖.这是一个随机事件 | ||
D、分别写有三个数字-1,-2,4的三张卡片,从中任意抽取两张,则卡片上的两数之积为正数的概率为
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com