
题目列表(包括答案和解析)
 如图,AD为⊙O的直径,作⊙O的内接等边三角形ABC.黄皓、李明两位同学的作法分别是:
如图,AD为⊙O的直径,作⊙O的内接等边三角形ABC.黄皓、李明两位同学的作法分别是:
| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| B.比较了解 | m |
| C.基本了解 | 45% |
| D.不了解 | n |
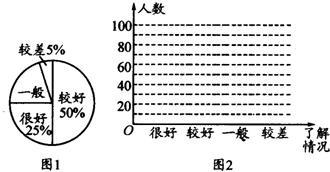 19、“安全教育,警钟长鸣”,为此某校从1400名学生中随机抽取了200名学生就完全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计形(如图).
19、“安全教育,警钟长鸣”,为此某校从1400名学生中随机抽取了200名学生就完全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计形(如图). 25、画图并讨论:
25、画图并讨论:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com