
题目列表(包括答案和解析)
阅读理解填空:
(1)如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
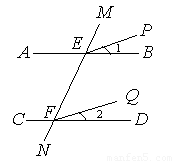
证明:∵AB∥CD,
∴∠MEB=∠MFD( )
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.( )
(2)如图,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD.

解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180 o( )
∵∠BAC=70 o,
∴∠AGD= 。
阅读理解填空:
(1)如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.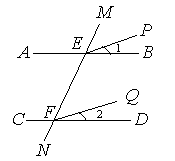
证明:∵AB∥CD,
∴∠MEB=∠MFD( )
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.( )
(2)如图,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD.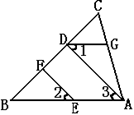
解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180 o( )
∵∠BAC=70 o,
∴∠AGD= 。
 22、填空或填写理由.
22、填空或填写理由. 22、填空或填写理由:
22、填空或填写理由:根据下列证明过程填空:
(1)如图,已知直线EF与AB、CD都相交,且AB∥CD,试说明∠1=∠2的理由.
解:∵AB∥CD (已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=∠2( 等量代换 )
(2)如图,已知:△AOC≌△BOD,试说明AC∥BD成立的理由.
解:∵△AOC≌△BOD
∴∠A= ( )
∴AC∥BD ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com